
剪枝+少量数据+少量训练=高效的Large Language Models压缩
大语言模型(LLMs, Large Language Models)在各种任务上展现出了强大的能力,这些能力很大程度上来自于模型巨大的参数量以及海量的训练语料。为了应对这些规模上存在的挑战,许多研究者开始关注大语言模型的轻量化问题。我们提出了一种基于结构化剪枝的方案,能够“物理地”移除冗余的结构和参数,同时保留大部分原模型已经学习到的参数,实现高效的大语言模型压缩。
LLM-Pruner: On the Structural Pruning of Large Language Models 【Arxiv】
Xinyin Ma, Gongfan Fang, Xinchao Wang
项目地址:
https://github.com/horseee/LLM-Pruner!!更新:支持了LLaMA-2和Baichuan的剪枝
首先,大语言模型的压缩与传统的神经网络(例如BERT, CNNs)的压缩等有什么差异呢。这需要从模型/数据/任务三个角度来分析:
- 模型规模:第一个主要差异来自LLM的巨大参数量,这导致许多侧重训练(Training-heavy)的压缩方案,例如知识蒸馏[1]变得较为困难.
- 海量训练语料:许多LLMs经历了1万亿甚至更大规模的tokens上的训练[3],这导致许多依赖于原始数据或收集替代数据的方案变得尤其昂贵。
- 任务无关的模型压缩:现有的压缩算法通常针对单一、特定的任务进行压缩,而LLMs是很优秀的多任务处理器,在压缩过程中我们不希望折损LLM的通用性和多功能性。
针对上述三种问题,我们需要一种能够避免大规模重新训练、且能保持模型原有能力的压缩方法。现有的较为可行的两种方案是【模型量化】和【结构化剪枝】。其中模型量化侧重于降低推理阶段的存储开销以及提升计算速度,而结构化剪枝则直接移除部分参数实现压缩,两种方案可以相互结合达到最优性能。本文主要介绍基于结构化剪枝的LLM压缩方法。
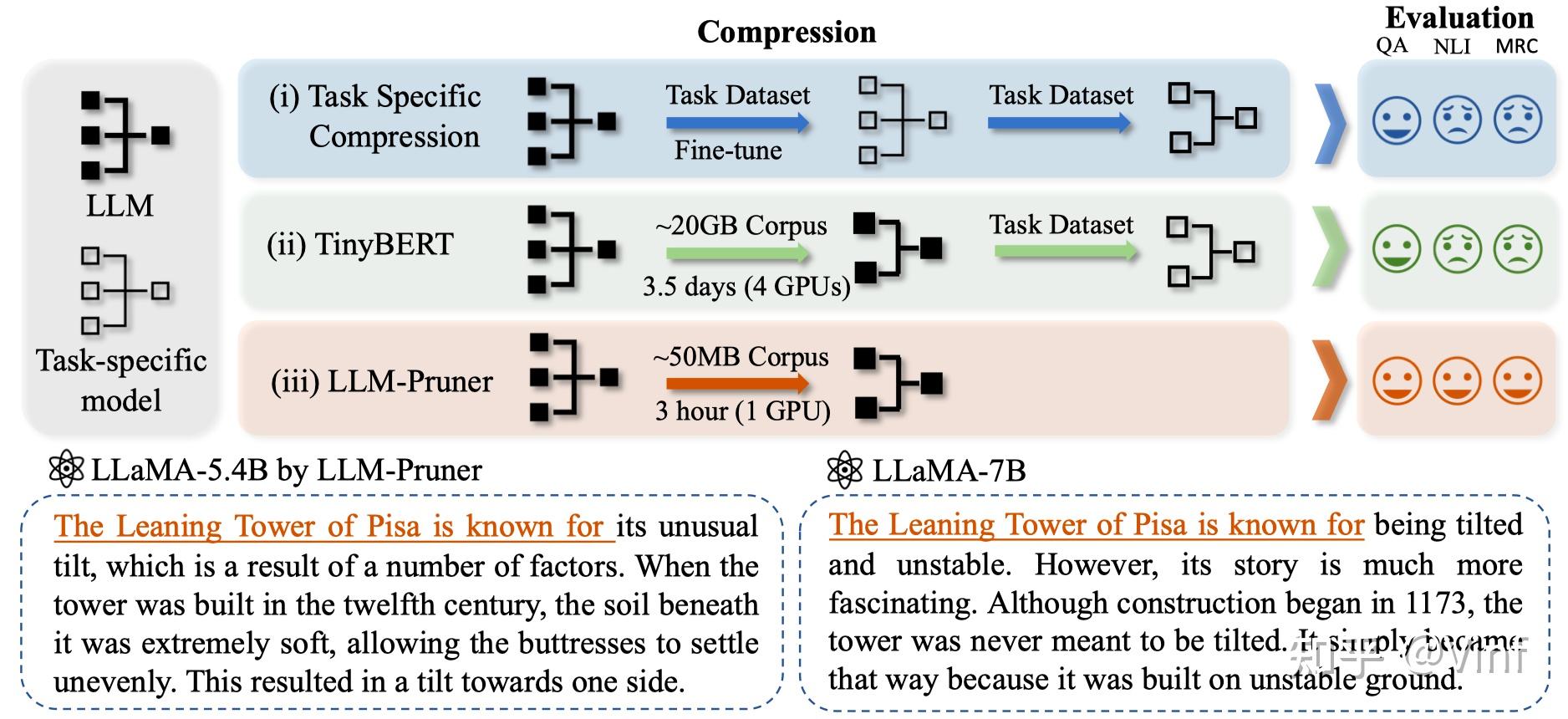
在本节中,我们提供了LLM-Pruner的详细解释。遵循常规的剪枝流程,LLM-Pruner包含三个步骤:发现阶段,估计阶段,恢复阶段。
(1) 发现阶段:这一步聚焦于识别LLM内部相互依赖的结构,这些相互依赖的结构需要被同时移除已确保剪枝后结构的正确性。
(2) 估计阶段:一旦耦合结构被分组,第二步就包含估计每个组对模型总体性能的贡献,并决定要剪枝的组。
(3) 恢复阶段:这一步涉及到快速的后训练,用于缓解由于结构删除而可能引起的性能降级。
类似于之前的研究[4],剪枝开始于为LLM的内部结构建立依赖性。假设 和
是模型中的两个神经元,
和
表示
输入、输出所指向的所有神经元。结构之间的依赖性可以定义为:
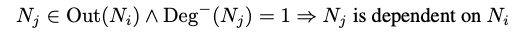
其中 表示神经元
的入度。注意到这种依赖性是方向性的,我们因此可以得到另一种依赖性:
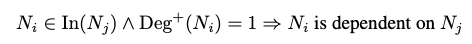
其中 表示神经元
的出度。依赖性在网络剪枝中的重要性在于,如果当前神经元(例如,
)仅依赖于另一个神经元(例如,
),且神经元
被剪枝,则神经元
也必须被剪枝。此时如果不裁剪
,那么网络结构中的维度就会不匹配。
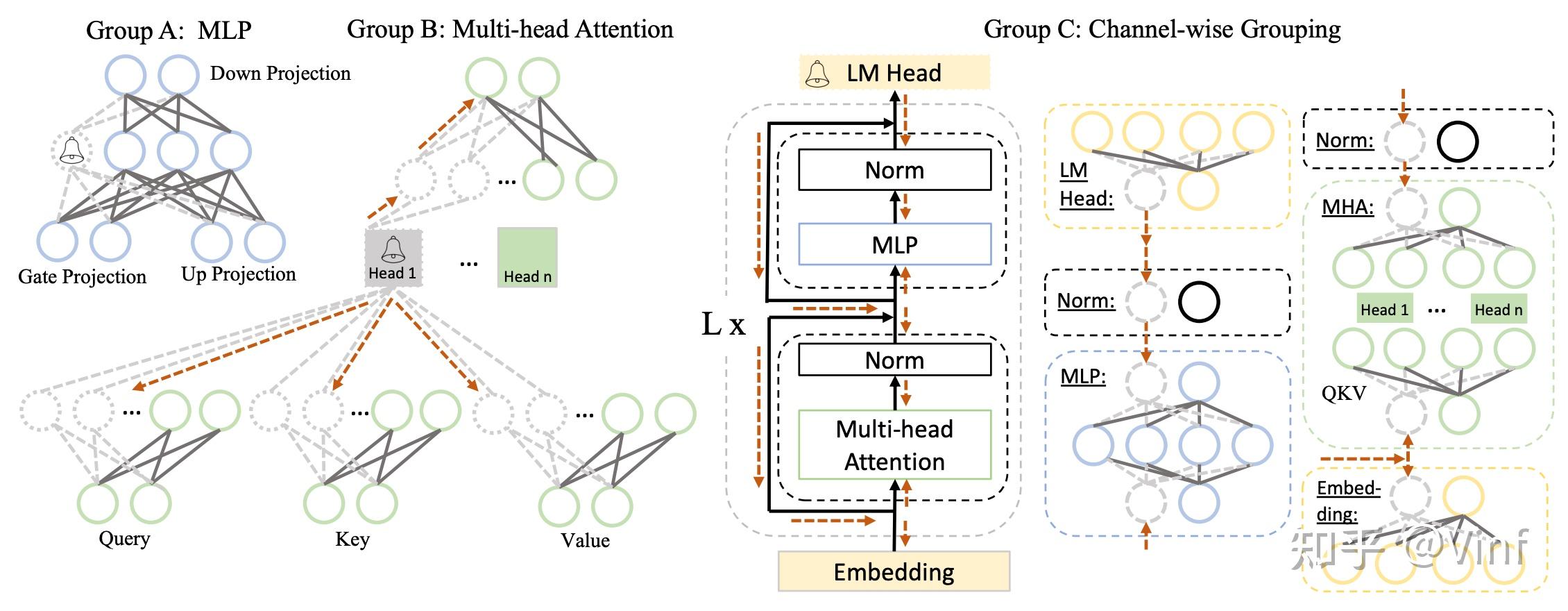
图2展示了LLaMA模型中存在的层耦合关系,主要由MLP内部的耦合、MHA内部的耦合(主要为QKVO四个映射层)与整个网络中的通道耦合。我们将上述耦合利用公式1和公式2整合成一个Dependency Graph[4],就能利用递归搜索快速在图中寻找到耦合结构了。
目前,我们已经对模型内部的耦合结构进行了分类。因此,我们评估一个组作为一个整体的重要性,而不是评估单个结构的重要性。鉴于对训练数据集的访问权限有限,我们探索使用可用的公共数据集或手动创建的样本作为替代资源。尽管这些数据集的领域可能与训练集不完全一致,但它们仍提供了评估结构组重要性的宝贵信息。
权重向量的一阶重要性估计。假设给定一个数据集 ,其中N是样本数量。在我们的实验中,我们设置N等于10,并使用一些公共数据集作为
的来源。一个组(如前所述,被定义为一组耦合结构)可以被定义为
,其中M是一个组中耦合结构的数量,
是每个结构的权重。在修剪时,我们的目标是移除对模型预测影响最小的结构,这可以通过损失的偏差来表示。特别地,为了估计
的重要性,损失的变化可以被表达为:
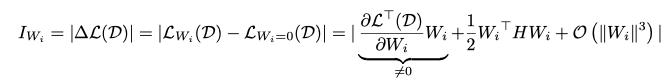
其中, 是Hessian矩阵。在这里,
表示next-token prediction loss。第一项在常规的剪枝文章中,由于模型在训练数据集上往往已经收敛,此项通常为0,即
。然而,由于
在这里并未从原始训练数据中提取,这意味着
(实验中发现loss高于充分收敛样本下的loss)。这为通过在LLMs下的梯度项确定
的重要性提供了一个理想的特性。然而,由于Hessian矩阵的计算复杂度过高,我们不直接对参数向量计算Hessian矩阵,而是仅考虑估计hessian矩阵的对角线元素,这需要引入单个参数标量的重要性评估。
单个参数的二阶重要性:上述过程对整个权重向量 的进行了估计。实际上,我们可以在更细粒度上得到另一种重要性度量,其中
内的每个参数都被独立地评估其重要性:
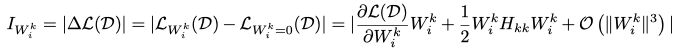
这里, 代表
中的第k个参数。我们使用Fisher Information Matrix来近似Hessian矩阵的对角线
,重要性可以被定义为:
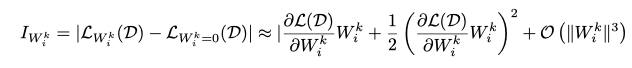
组重要性:通过利用 或
,我们估计了参数或权重的粒度上的重要性,且同时利用了模型的一阶、二阶梯度信息,然而我们还需要将其扩展到整个分组
。本文以四种方式集成重要性得分:
- 求和:
或
;
- 乘积:
或
;
- 最大值:
或
;
- 门控(组内最后一层):
或
,其中
是每个分组内最后的结构。
在评估每个组的重要性之后,我们根据预定义的修剪比例对每个组的重要性进行排序,并修剪重要性较低的组。上述聚合方式实际上包含了不同的偏置,例如求和策略认为不同参数的贡献是独立且可叠加的,乘积策略则假设不同层的重要性会相互影响,最大值策略的偏置在于层的重要性由某一层主导。最后,门控策略则认为组内的最后一层主导了整个组的重要性,因为通过将该层设为0我们可以使得整个组不再参与网络预测。
为了加速模型的恢复过程并在有限数据下提高其效率,最小化恢复阶段需要优化的参数量是至关重要的。为了便于此,我们采用低秩近似LoRA对剪枝后的模型进行后训练。模型中的每个可学习的权重矩阵,表示为 ,包含LLM中所有剪枝和未剪枝的线性投影。
的更新值
可以被分解为
,其中
和
。前向计算现在可以表达为:
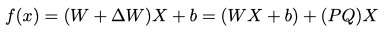
其中b是稠密层中的偏置。仅训练P和Q减少了整体训练复杂性,从而减少了对大规模训练数据的需求。此外,额外的参数P和Q可以被重新参数化为 ,这不会在最终压缩模型中造成额外的参数。
上述过程给出了LLM模型的依赖分析、重要性评估以及后训练的完整方案,通过集成一阶和二阶泰勒展开,我们可以得到更加鲁棒的重要性评估策略。对于大模型而言,重要性评估指标是尤其重要的,因为剪枝造成的性能损失越大,后训练恢复所需要的数据量、训练时间也就越多。
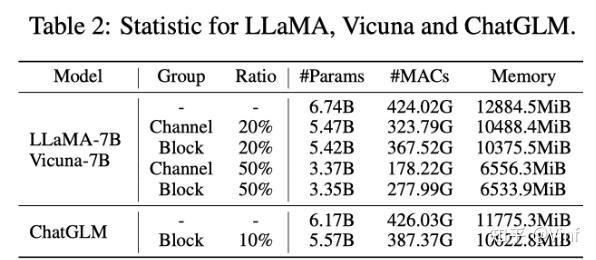
本文对三种开源的LLM进行剪枝实验,包括LLaMA-7B, Vicuna-7B和ChatGLM,剪枝前后的模型参数量、MACs和内存占用如表所示。原始的LLaMA-7B模型在不使用额外量化等技术的情况下,在24GB单卡上仅能执行推理操作,而剪枝后的小模型我们可以使用单卡24GB完成微调。
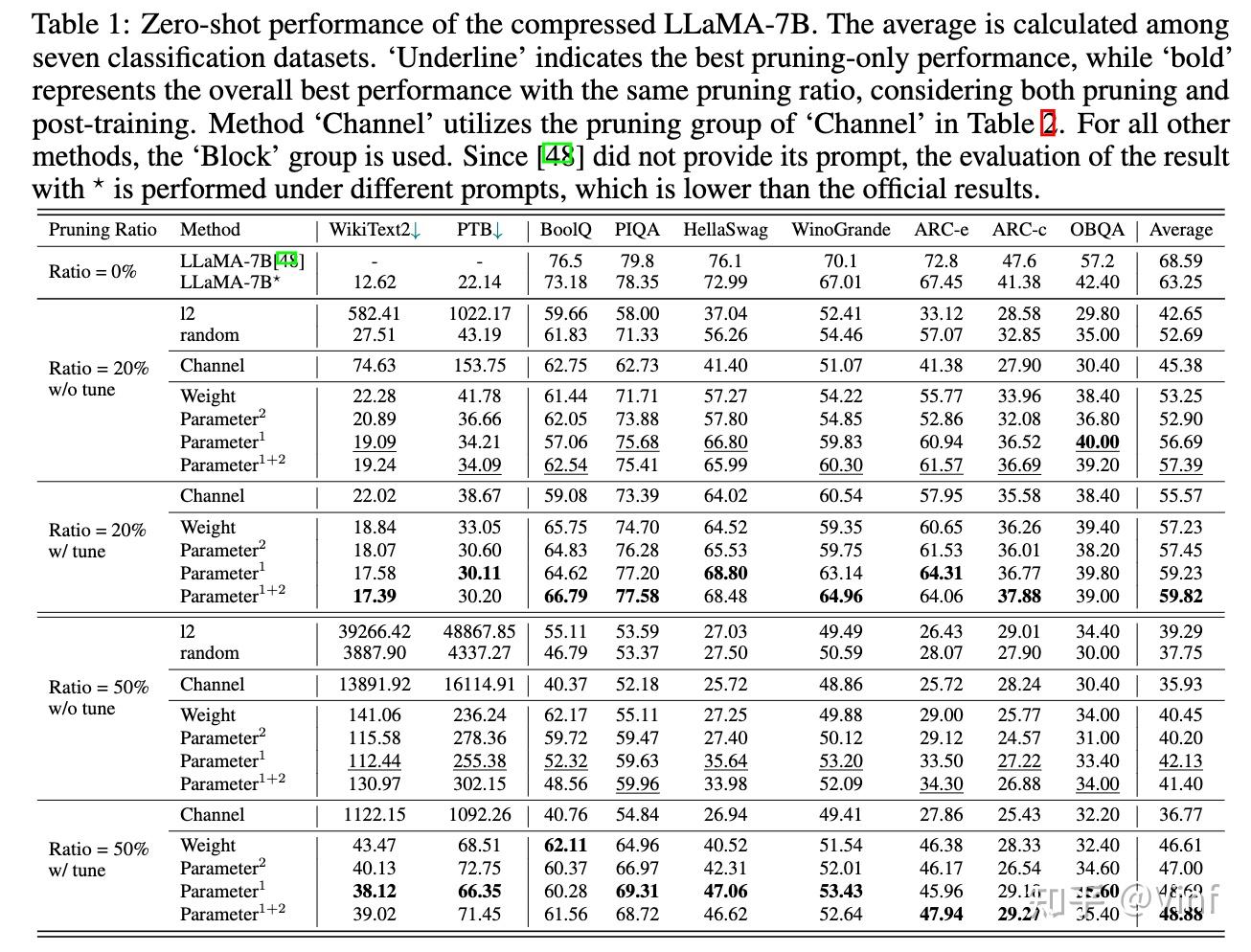
对于大模型而言,保留原始的多任务处理以及零样本能力是尤其重要的,我们完整评测了不同多种方案,包括权重剪枝、随机剪枝以及本文方法的剪枝效果。我们发现在剪枝20%参数的情况下,大模型依旧能保持一定的zero-shot能力,同时经过少量微调,zero-shot性能可以快速提升。
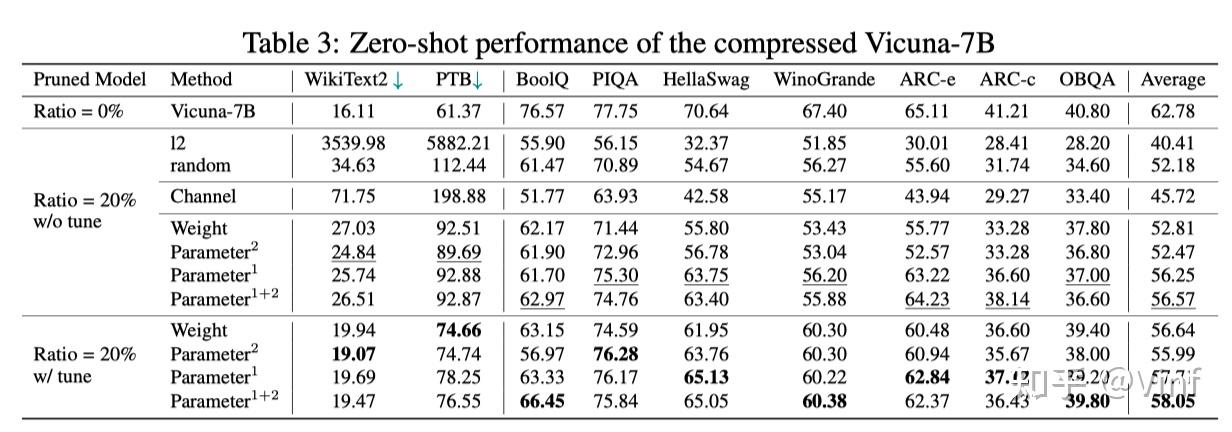
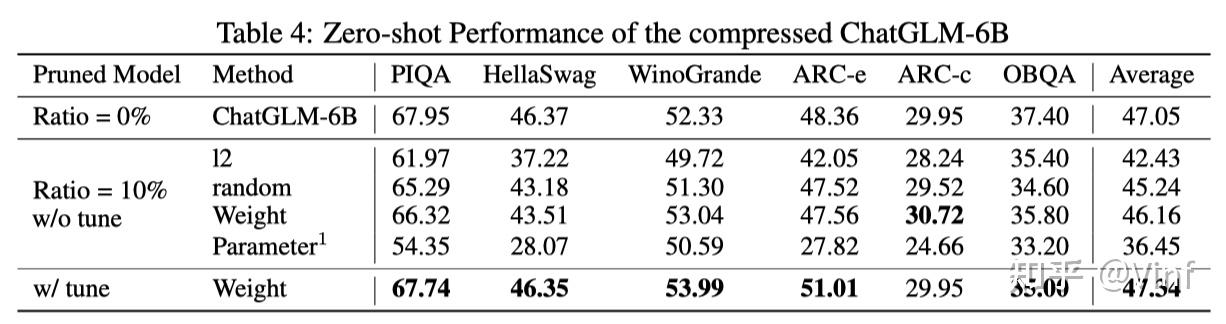
以下表格展示了不同剪枝后模型的生成文本质量,可以发现微调后的模型依旧维持了较好的生成能力

- Gou, Jianping, et al. "Knowledge distillation: A survey."International Journal of Computer Vision129 (2021): 1789-1819.
- He, Yang, and Lingao Xiao. "Structured Pruning for Deep Convolutional Neural Networks: A survey."arXiv preprint arXiv:2303.00566(2023).
- Hoffmann, Jordan, et al. "Training compute-optimal large language models."arXiv preprint arXiv:2203.15556(2022).
- Fang, Gongfan, et al. "Depgraph: Towards any structural pruning."arXiv preprint arXiv:2301.12900(2023).


 上一篇
上一篇 



