数学优化(mathematical optimization)是研究优化问题的数学理论和方法 的_门学科.优化问题,顾名思义,就是在众多可能中寻找最优解的问题.在数学 上,优化问题通常建模成在一定条件下寻求满足某种最优性质的解.数学优化在 早期被称为数学规划(mathematical programming).英文“programming”—词 是多义词,大众更多的是知道其“程序”含义而不是“规划”.所以,近年来国际 数学界更偏向用数学优化取代数学规划.标志性的事件是国际上最重要的数学 优化学术组织,成立于1973年的“数学规划学会”(Mathematical Programming Society),在2010年经全体会员投票决定更名为“数学优化学会”(Mathematical Optimization Society).
数学优化是数学的一个重要学科方向,是应用数学的重要组成部分.例如, 美国工业与应用数学学会(Society on Industrial and Applied Mathematics, SIAM) 就下设优化分会,且主办了国际著名学术期刊SIAM Journal on Optimization. 运筹学(英:operational research;美:operations research)是研究决策的科学, 其核心就是数学优化.正因为如此,数学优化被看成运筹学的分支【I在国内 外重要的运筹学学术组织中,如国际运筹学联合会(International Federation of Operational Research Societies) > 美国运筹学与管理科学研究协会(Institute for Operations Research and the Management Sciences) > 中国运筹学会等,数学优 化都是非常活跃、重要的研究方向和分支.特别是在我国,中国运筹学会规模最 大、影响最大的专业委员会就是数学规划专业委员会.数学优化中研究优化问 题数值方法的分支称为数值优化,它与数值代数、数值微分方程并列为数值分 析的三大分支.数值优化方法是科学计算的基础之一.优化计算方法是计算数 学的重要组成部分.数学优化还是管理科学的基本方法和技术之著名数学家欧拉曾说过,“宇宙间万物无不遵循某种最大或最小准则”.优化 理论与方法在国防、经济、金融、工程、管理等许多重要领域都有直接的应用. 例如,在金融经济领域,期权定价、投资组合、风险估计等都可归结为优化问题. 很多其他自然科学领域的科学问题也可归结为优化问题.例如,生命科学中的蛋 白质折叠、DNA序列分析、基因比对等问题本质上都是优化问题;信息科学中 的图像处理和模式识别关键在于优化问题的计算;地球科学中天气预报和石油 勘探的核心问题也都是优化问题;在材料科学领域,电子结构计算、复合材料设 计的难点在于求解优化问题;化学科学中的催化反应问题等通常也建模为优化 问题;大数据处理、分析、预测等都离不开优化方法.
数学优化的历史至少可以追溯到法国数学家费马(Pierre de Fermat, 1601_ 1665),他在给罗贝瓦尔(G. P. Roberval, 1636年)和笛卡儿(1638年)的信中 提出求极大、极小值的步骤,本质上就是通过求稳定点来找极值点. 1669年, 牛顿在文章 De analyst per aequationes ngumero terminorum infinitas 中提出的 方程求根方法后来发展成为非线性方程组和无约束优化的基本算法.莱布尼茨 于1684年发表了题为《一种求极大值与极小值和切线的新方法,它也适用于分 式和无理量,以及这种新方法的奇妙类型的计算》的文章.牛顿在1687年出版 的《自然哲学的数学原理》一书的前言中写道,“十年前在我和最杰出的几何学 家莱布尼茨的通信中,我表明我已经知道确定极大值和极小值的方法、作切线 的方法以及类似的方法,但我在交换的信件中隐瞒了这个方法……”,这位最 卓越的科学家在回信中写道,“他也发现了一种同样的方法,并诉述了他的方法, 该方法除了措辞和符号之外与我的方法几乎没有什么不同”.在1713年该书第 二版中牛顿依然保留了这段话,但在1726年第三版及以后的各版中,这段话就 被删掉了.这段话通常被用来考证牛顿与莱布尼茨创立微积分之争(现在,人 们公认牛顿和莱布尼茨各自独立地创建了微积分).我们从这段话可以看出,研 究优化问题不仅是微积分最早期的应用之一,同时也对微积分的创立起了一定 的驱动作用.早期关于优化问题的著名研究还包括拉格朗日(1736—1813)处理 等式约束的乘子方法,高斯(1777—1855)关于非线性最小二乘的方法以及柯西 (1789—1857)提出的最速下降法.
现代数学优化诞生于20世纪上半叶第二次世界大战中[2】. 1939年,康托 洛维奇(1912-1986)发展了线性规划方法来合理安排资源调配,以减少军队开 支和扩大敌方损失.几乎同时,Koopmans (1910一1985)将经典经济问题建模成 线性规划.后来,他们共同获得了 1975年的诺贝尔经济学奖.第二次世界大 战期间,他们的工作没有及时被科学界广泛知晓.真正推动线性规划发展的是 George Dantzig (1914一2005),他没有像同时代的经济学家那样只把线性规划用 来建模和分析经济现象,而是把线性规划看成求解一类特殊实际问题之最优解 的方式.1947年,Dantzig发明了求解线性规划的单纯形法.也因为如此,优化 界公认他是数学规划之父.单纯形法(simplex method)是20世纪科学计算中最 重要的算法之一.
现代非线性规划兴起的标志性工作是Kuhn (1925—2014)和Tucker (1905—1995)在1951年所给出的约束优化最优性条件【3】.非线性规划这一概念也是在 此文首次被提出.正因为如此,Kuhn和Tucker被认为是非线性规划的先驱.事 实上,约束优化的最优性条件早在1939年就由Karush (1917—1997)在其硕士 学位论文中提出并深入研究.虽然Karush的工作在很长一段时间内不为优化界 所知,但是他的首创贡献最终还是被广泛认可.现在,约束优化的最优性条件被 优化界称为KKT条件,即由上述三位先驱姓氏的首字母组成.
整数规划早期的最著名研究是由Markowitz和Manne合作于1957年发表 在著名期刊Econometrica上的文章,该文给出了分支定界的概念和技术. Markowitz (1927—)在金融经济学方面的工作于1990年获得诺贝尔经济学奖. 整数规划的一个重要技术是割平面法,该方法由Gomory (1929—)于1958年 提出.分支技术和割平面技术相结合逐渐成为求解整数规划和组合优化的主 要方法.离散优化除了经典的整数规划还包括组合优化与网络优化.离散问 题由于其特殊结构,许多问题都是NP-难的,吸引了许多著名学者对其进行研 究,代表性人物包括中国运筹学会前理事长越民义先生以及德国数学会前会 长、国际数学联盟前秘书长、柏林科学院院长、中国科学院外籍院士 Martin Groetschel.
从现代数学优化的诞生到20世纪末,数学优化的不少研究成果产生了非常 重要的影响.除了上述提及的单纯形法和KKT条件,还有20世纪50年代的共 辗梯度法、60年代的拟牛顿法和增广拉格朗日函数法、70年代的信赖域法、80 年代的内点法以及BB步长梯度法等.进入21世纪后,数学优化发展势头依然 强劲,涌现出了许多新的方法和技术,一些早期技术在新问题上得到了广泛的应 用,如Nesterov加速技术、Lassarre松弛技术、ADMM方法和随机梯度法等.在 学科发展上,数学优化从线性规划、非线性规划的兴起逐步发展到多个分支方 向,如整数规划、组合优化、变分不等式与互补问题、向量优化、非光滑优化、 随机优化、动态规划、半定规划、锥优化、多项式优化等.近年来,受应用的驱 动,数学优化的新热点和新方向不断涌现,如稀疏优化、鲁棒优化、在线优化、 张量优化、流形上的优化、机器学习中的优化等.
优化与数学的各分支都有密切的联系.分析数学的方法,特别是数值泛函分 析对研究优化方法的理论性质,如收敛性、收敛速度等至关重要.而数值代数是 数值优化的核心部分,所以优化方法的构造离不开数值代数.由于求函数极值 在几何上是求解曲面上的最高点或最低点,函数的几何性质对寻找好的优化方 法有很好的指导作用.基础数学的理论和结果对数学优化有深刻的影响.例如, 共辗梯度法就是由著名几何学家Stiefel (1909-1978)和曾任美国数学会副会长 的著名数学家Hestenes (1906-1991)合作提出的;组合优化的匈牙利算法是基 于矩阵组合性质的Egervary定理,而Egervary (1891一1958)是匈牙利著名数学 家,曾获匈牙利国家科技最高奖Kossuth奖;多项式优化与Hilbert (1862—1943) 第17问题有密切联系,关于多项式优化的研究,依赖于代数中的许多纯理论结 果;近年来逐渐受到重视的流形上的优化的研究,则需要利用流形上的几何性 质.统计和优化联系同样非常密切,许多实际问题利用统计方法建立的模型大 多是优化问题.数学优化在其他领域的渗透也在加强.例如,在通信领域,信号 处理中的资源配置问题都离不开优化方法;在经济金融领域,几乎所有的数学模 型都是优化模型;在数据科学领域,优化是最基本的分析手段和工具之一.人工 智能、机器学习中的主要方法之一就是优化.
从事数学优化研究的科研人员分布在高等学校、科研院所、企业、金融机 构等.在欧洲,高等学校中研究数学优化的专家大多集中在数学系或应用数学 系.但在美国,数学优化的专家既有人就职于数学系,也有人就职于运筹系、工 程系、管理系等.美国的很多大型企业旗下的研究机构,如IBM的Watson研 究中心、朗讯的贝尔实验室等都拥有著名的数学优化研究人员.我国的一些著 名企业,如华为、阿里巴巴、滴滴等都在其下设的研究部门聘有相当数量的从事 数学优化研究的高水平专家.
在国际学术界,数学优化近年来也越来越受到重视.最近的几次国际数学家 大会和国际工业与应用数学大会上都有数学优化方面的邀请报告.数学优化已 逐渐成为数学的一个重要方向,它吸引了不同数学分支的专家的关注.近年来 在国际上备受重视的压缩感知问题本质上是一个特殊的优化问题,菲尔兹奖获 得者陶哲轩等对该问题就有深入研究.悬赏百万美元的Netflix问题实质上是低 秩矩阵完整化问题,通常也被建模成一个特殊的优化问题.
国际上最著名的优化学术期刊是创刊于1971年的Mathematical Programming, 它是国际数学优化学会的会刊.数学优化的另一个顶尖刊物是美国工业 与应用数学学会主办的、创刊于1990年的SIAM Journal on Optimization.国际 最重要的数学优化学术会议是由数学优化学会主办的三年一度的国际数学规划 大会(International Symposium on Mathematical Programming). 另夕卜个日E常 重要的数学优化方面的学术会议是美国工业与应用数学学会主办的SIAM优化 会议(SIAM Conference on Optimization),它也是三年举行一次 数学优化界的 最高奖是由美国工业与应用数学学会和国际数学优化学会联合颁发的Dantzig 奖.该奖设立于1979年,每三年颁发一次,1982年首次颁奖,获奖者为Powell (1936一2015)和 Rockafellar (1935).
近年来,优化方法的应用在国际上越来越普遍,同时也受到越来越高的重 视.在2012年美国科学院出版的美国国家研究理事会组织编写的《2025年的数 学科学》[4]中,多处提到了优化方法的应用.例如,在该书的3.6节“数学科学 对工业的贡献”中写道:“半导体行业利用优化方法,设计计算机芯片,以及模 拟材料的生产过程和性能书中还指出,欧洲科学基金会2010年的《数学与工 业》报告把优化方法列为数学在工业中成功的应用案例之一.报告指出:“随着 计算能力的提高和加速算法上取得成绩的增多,产品优化已成为现实,这对于工 业至关重要. ” 2012年美国白宫科学与技术政策办公室的报告《捕捉先进制造 业的国内竞争优势》确定了 11个交叉技术领域,是R&D投资的最佳获选领域, 这些领域在很多方面都依赖系统的建模、大量数据的分析、控制和优化.当前 国际上备受重视的人工智能、机器学习等领域所归结的核心问题就是优化,所 以优化在这些领域将得到更广泛的应用和发挥越来越重要的作用.未来,自动 驾驶技术、智能医生系统、无人作战系统等各种机器取代人的系统能得到很好 的实现必将依赖高度复杂的、多目标的、在线的、随机优化问题的快速求解,有 的可能还要依赖于建立目前我们尚不知道的新类型的优化问题以及这些问题的 快速求解.当然,等量子计算机被广泛应用时,优化问题的算法设计和理论分析 无疑也会发生翻天覆地的变化.这一天应该迟早都会到来,但我们等待的时间 将取决于未来科技发展的速度.
在中国,“田忌赛马”是运筹应用的一个很好的实例.从“运筹帷幄之中,决 胜千里之外”可知运筹思想在我国古代军事中就早有应用.公元前6世纪的《孙 子兵法》是我国古代军事运筹思想最早的典籍.现代运筹学被引入中国是在20 世纪50年代后期岡.在钱学森、许国志等的积极推动下,1956年中国科学院力 学研究所成立了运筹学小组.该小组后来并入中国科学院数学研究所的运筹学 研究室.我国数学优化的起源可追溯到1958年,那时华罗庚投身“大跃进”运 动,发展应用数学,促进数学在实际中的应用.他带领学生走访运输部门,推动 运筹学方法的运用,其中一个代表性的工作是“打麦场的选址问题1960年,管 梅谷发表在《数学学报》的论文中提出邮递员选择最优路径问题,后来被国际同 行称为“中国邮递员问题”.这是我国在数学优化领域第一个有着重要国际影响 的工作.在“文化大革命”期间,华罗庚和他的小分队去农村、工厂、矿山推广优 化技术和统筹方法,足迹遍布中国大江南北.其中普及最广的是“黄金分割法”, 俗称0.618法.这个求解单变量优化问题的简单方法可能是世界上最广为人知 的一个优化算法.统筹方法的推广和普及推动了若干数学优化方法在生产实际 中的应用,为我国国家建设和国民经济做出了重要贡献.
改革开放以来,我国在数学优化方面的研究有了长足的进步,在既约梯度 法、非线性共辗梯度法、信赖域方法、拟牛顿法、子空间方法、交替方向方法、 稀疏优化、张量优化等多个方向上取得了突出的成绩,涌现了一批非常优秀的 青年优化学者.在海外有一批数量可观、非常杰出的华人优化专家,他们对我国 数学优化的学科发展和人才培养发挥了重要的作用.
我国运筹学会的会刊 Journal of the Operations Research Society of China 创刊于2013年,至今所发表的文章大多都是关于数学优化方面的.中国运筹学 会数学规划分会是中国运筹学会最大的分会,每两年召开一次年会,年会参加人 数通常为600~800人.
本书后面各章将分析目前数学优化的主要分支、核心前沿方向、当前进展 及发展态势,包括当前热门研究课题、主要的思想、方法与技巧、主要的难题, 以及近年来的主要成果与活跃的前沿人物;提出对学科发展态势的观点与看法; 凝练出本学科的基本思想、核心方法与关键技巧;根据我国学科发展和国家重 大需求,凝练与该学科密切相关的重要问题,建议、组织攻关和研发队伍,解决 重大理论或实际问题;为我国优化学科发展提出整体建议.
希望本书能推动我国在数学优化的学科建设和人才培养,为提高我国数学 优化的研究水平和促进该学科在其他领域的应用做出贡献.
参考文献
[1]中国科学技术协会,中国运筹学会.2012-2013运筹学学科发展报告.北京:中国科 学技术出版社,2014.
[2]Groetschel M. Documenta Mathematica. Extra Volume: Optimization Stories, 2012.
[3]Lenstra J K, Rinnooy Kan A H G, Schrijver A. History of Mathematical Programming. A Collection of Personal Reminiscences. Amsterdam: North- Holland, 1991.
[4]美国科学院国家研究理事会.2025年的数学科学.刘小平,李泽霞,译.北京:科学出 版社,2014.
[5]华罗庚,苏步青.中国大百科全书:数学.北京:中国大百科全书出版社,1988.
第2章
线性规划
2.1线性规划问题背景
线性规划(linear programming, LP)泛指研究目标函数和约束条件都是线 性函数的最优化理论与算法及应用,是最优化理论中非常重要的一类优化问题, 它在形式上是最简单且最具广泛应用的数学优化问题.一个线性规划问题是在 可行域为多面体和多胞形上极小化或者极大化线性目标函数.线性规划在经济 管理、金融、军事、交通运输、工业等领域有着广泛的应用,为合理地利用有限 的人力、物力、财力等资源做出最优决策提供科学的方法.
线性规划起源于第二次世界大战军事作战的需求,是现代数学优化的起源 和标志.第二次世界大战期间,英、美的军队中成立了运筹学研究小组,开展了 护航舰队保护商船的编队问题和当船队遭受德国潜艇攻击时,如何使船队损失 最小问题的研究.线性规划这一概念是在同军事行动计划有关的实践中产生的. 1947年在美国海军工作的数学家G. B. Dantzig提出求解线性规划的单纯形法, 为解决美国和盟国军事问题以及赢得战争最后的胜利做出了巨大贡献,同时奠 定了线性规划这门学科的基础E.单纯形法被科技界公认是20世纪的十大算法 之一.在此之前,已有很多数学家对线性规划的发展应用以及线性规划作为一门 学科的诞生做出了多方面的贡献.关于线性规划的早期研究可以追溯到法国数 学家傅里叶(J. B. J. Fourier, 1768一1830)和 Vallee-Pousson,他们分别于 1823 年和1911年独立提出线性规划的想法,但未引起注意.1896年Farkas提出了 有限个线性系统的择一性定理,后续很多数学家做了一系列关于线性规划的工 作.例如,1911 年与 1934 年 Pousson 和 Motzkin 分别提出了 Fourier-Motzkin 消元法;1932年Haar证明了对于无限个线性系统的择一性定理;等等.1938年 苏联数学家Kantorovich提出线性规划模型的经济学概念,出版了《生产组织与 计划中的数学方法》一书,对列宁格勒胶合板厂的计划任务建立了一个线性规 划的模型,并提出了 “解乘数法”的求解方法,为数学与管理科学的结合做了开 创性的工作,Kantorovich因此获得了诺贝尔经济学奖.还有不少数学家也在线 性优化方面做出了重要贡献,如Karush、Hitchkock、Koopmans等等.然而具 有里程碑意义的工作当属Dantzig在1947年提出的求解线性规划的单纯形法, 真正为线性规划学科奠定了基础.同在1947年,20世纪最重要的数学家之一 冯.诺依曼(J. von Neumann, 1903一1957)提出了线性规划的对偶理论,开创了 线性规划的许多新的研究领域,扩大了它的应用范围和解题能力.1951年美国 经济学家Koopmans把线性规划应用到经济领域,为此与Kantorovich 一起获 得了 1975年诺贝尔经济学奖囲.
1950年后国际学者们对线性规划进行大量的理论研究,并涌现出_大批新 的算法.例如,1954年Lemarechal提出对偶单纯形法,1954年Shetty等解决了 线性规划的灵敏度分析和参数规划问题,1956年Tucker提出互补松弛定理,1960 年Dantzig和Wolfe提出分解算法等3,句.1979年苏联数学家L. G. Khachiyan (1952-2005)提出解线性规划问题的椭球算法,并证明它是多项式时间算法回. 1984年美国贝尔电话实验室的印度数学家Karmarkar提出解线性规划问题的 新的多项式时间算法.用这种方法求解线性规划问题在变量个数为5000时只要 单纯形法所用时间的1/50.现已形成线性规划多项式算法理论【6】.随着21世纪 来临,线性规划被推广到线性锥规划,把关于线性规划多项式时间的算法推广到 具有凸锥结构的非线性规划问题上.线性规划的研究成果还直接推动了其他数 学规划问题,包括整数规划、随机规划和非线性规划的算法研究.随着计算机的 发展,出现了许多线性规划的软件,如MPSP、OPHEIE、UPPIRE、CPLEX、 XPRESS、GUROBI等,可以方便地求解几万个变量或约束线性规划问题.
由于很多实际问题可用线性规划描述和近似,线性规划通常可用于研究资 源的最优利用、设备最佳运行等问题.例如,当任务或目标确定后,如何统筹兼 顾,合理安排,用最少的资源(如资金、设备、原材料、人工、时间等)去完成 确定的任务或目标;企业在一定的资源条件限制下,如何组织安排生产获得最好 的经济效益(如产量最高、利润最大).因此线性规划是运筹学中研究早、发展 快、应用广泛、方法最成熟的重要分支.进一步,在求解非线性规划和整数规 划等优化问题的过程中,必须用到线性规划,使得线性规划成为科学管理的一种 基本的数学方法,广泛应用于军事作战、经济分析、经营管理和工程技术等方 面.它为合理地利用有限的人力、物力、财力等资源做出最优决策,提供科学 依据.
2.2线性规划数学模型
线性规划数学模型由决策变量(decision variable)、目标函数(objective function) 及约束条件(constraint)构成.其中目标函数是由多个决策变量组成的线 性函数,通常是求最大值或最小值.解决问题的约束条件是多个决策变量的一组 线性不等式或等式.
标准的线性规划问题通常有如下表达式:
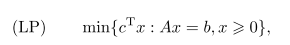
这里A是秩为m的mxn矩阵是m维的向量,c是九维的向量.
线性规划的基本概念主要是几种解的定义与关系.首先,关于约束矩阵A 中的基(basis)的概念,设B为A中mxm子矩阵且秩为m,称3是线性规 划的一个基(或基矩阵(basis matrix)).当m=n时,基矩阵唯一;当m <n时, 基矩阵就可能有多个,但数目不超过
 当确定某一基矩阵时,则基矩阵对应 的列向量称为基向量(basis vector),其余列向量称为非基向量,基向量对应的变 量称为基变量(basis variable),非基向量对应的变量称为非基变量.
当确定某一基矩阵时,则基矩阵对应 的列向量称为基向量(basis vector),其余列向量称为非基向量,基向量对应的变 量称为基变量(basis variable),非基向量对应的变量称为非基变量.
 当确定某一基矩阵时,则基矩阵对应 的列向量称为基向量(basis vector),其余列向量称为非基向量,基向量对应的变 量称为基变量(basis variable),非基向量对应的变量称为非基变量.
当确定某一基矩阵时,则基矩阵对应 的列向量称为基向量(basis vector),其余列向量称为非基向量,基向量对应的变 量称为基变量(basis variable),非基向量对应的变量称为非基变量.
线性规划的几种解包含:可行解(feasible solution)、最优解(optimal solution)> 基本解(basis solution)、基可行解(basis feasible solution)> 非可行 解(infeasible solution)和无界解(unbound solution).
线性规划的主要理论是解的最优性条件和对偶理论,分别介绍线性规划解 的基本定理和对偶理论如下.
(1)若线性规划问题存在可行解,则问题的可行域是凸集.
(2)线性规划问题的基可行解矛对应线性规划问题可行域(凸集)的顶点.
(3)若线性规划有最优解,则必存在一个基可行解是最优解.
线性规划问题的对偶问题有如下表达式:
这里g是m维的对偶变量,s是n维的互补松弛变量.
线性规划的对偶理论如下所述.
(1)弱对偶性:设g分另。为(LP)与(LD)的可行解,则户a; 2 bTy.
(2)在互为对偶的两个问题中,若一个问题可行且具有无界解,则另一个问 题无可行解.
(3)强对偶性:设蛆,g*分别为(LP)与(LD)的可行解,则x*,y*是(LP) 与(LD)的最优解当且仅当c^x*=bTy*.
(4)若互为对偶的两个问题其中一个有最优解,则另一个也有最优解,且最 优值相同.
(5)互补松弛定理:设蛆,g*分别为(LP)与(LD)的可行解,设%和% 分别是它的松弛变量的可行解,则麥,y*是(LP)与(LD)的最优解当且仅当 sjx*=0 和 Syy*=0.
2.3线性规划求解方法
求解线性规划问题的基本方法是单纯形法和内点算法.对于只有两个变量 的简单的线性规划问题,也可釆用图解法求解.这个方法的特点是直观而易于 理解,但实用价值不大.当然还有一些其他的方法,如Dikin步骤算法.在这里 我们不作介绍,有兴趣的读者可参考文献[4].
2.3.1单纯形法
单纯形法(simplex method)是求解线性规划问题的主要方法.首次提出这 个方法的是线性规划的集大成者DantzigM, 1947年,面对美国制订空军军事规 划时提出的问题,Dantzig首次提出了单纯形法来解决这类极值问题的求解.单 纯形法是最早求解所有一般线性规划问题的可行算法.根据线性规划的最优性 条件,最优解必在可行解集合的某个顶点上到达.因此算法的设计思想是先从 个初始基可行解出发,并判断它是否最优,若不是最优,再换一个基可行解并判 断,直到得出最优解或无最优解.它是一种逐步逼近最优解的迭代方法.
单纯形法求解线性规划问题的计算步骤包括最优性检验公式、入基公式、 出基公式,以及无解的判断和终止准则.如下是具体的步骤:
(1)求初始基可行解,列出初始单纯形表.
(2)最优性检验:当检验数勺一知W 0,且基变量中不含人工变量时,基可 行解为最优解,计算结束;当存在检验数勺—勺> 0时,如果有Pj < 0,则问题 为无界解,计算结束,否则转(3).
(3)从一个基可行解换到相邻的使目标函数值更小的基可行解,列出新的单 纯形表,确定出基变量.
(4)重复(2), (3)两步,一直到计算结束为止.
1953年,Dantzig为了修正单纯形法每次迭代中积累起来的进位误差,提出 了改进单纯形法.其基本步骤和单纯形法大致相同,主要区别是在逐次迭代中 不再以高斯消去法为基础,而是由旧基阵的逆去直接计算新基阵的逆,再由此确 定检验数.这样做可以减少迭代中的累积误差,提高计算精度,同时也减少了在 计算机上的存储量.
1954年美国数学家Lemarechal提出对偶单纯形法(dual simplex method). 单纯形法是从原始问题的一个可行解通过迭代转到另一个可行解,直到检验数 满足最优性条件为止.对偶单纯形法则是从满足对偶可行性条件出发通过迭代 逐步搜索原始问题的最优解.在迭代过程中始终保持基本解的对偶可行性,而 使不可行性逐步消失.当原始问题的一个基本解满足最优性条件时,其检验数 cbB-^A - c W 0,即知g=cbBT (称为单纯形算子)为对偶问题的可行解.满 足对偶可行性,即指其检验数满足最优性条件.因此在保持对偶可行性的前提 下,当基本解成为可行解时,便也就是最优解.
单纯形法的成功激发了众多的数学研究,焦点集中在如何选取下一个顶点, 即转轴规则(so-called pivot rules).由此引发的问题有很多,比如,是否存在一 种多项式时间迭代的转轴规则,是否存在一个线性规划问题需要指数时间的迭 代.1972年Klee和Minty回答了后面的问题,指出单纯形法不是多项式时间 算法叽两个新算法的出现打破了单纯形法独霸求解线性规划问题的地位.首先 是Khachiyan在1979年提出了椭球算法(ellipsoid algorithm).基于椭球算法, Khachiyan证明了线性规划问题属于一类多项式时间可解问题.虽然椭球算法 有很好的计算复杂性的理论结果,但是具体求解问题时计算效率非常差.第二 个算法是著名的内点算法,在1984年由在美国贝尔实验室工作的印度籍学者 Karmarkar 提出.
目前来看,随着大数据、云计算、人工智能时代的来临,求解大规模优化问 题是必需的.单纯形法由于维数限制,它的用处受到制约.然而,到目前为止,单 纯形法是数学规划中最经典、被研究最透彻、商业化最成熟的方法.
2.3.2内点算法
内点算法(interior point method)是多项式时间可解的数学规划问题.
1984年Karmarkar首次提出了投影内点算法,是多项式时间算法,从计算 复杂性、求解实际问题的有效性,以及处理大规模和稀疏问题的能力和速度等 方面,全面超越Khachiyan的椭球算法.自从Karmarkar内点算法问世,在优化 领域引起相当大的关注,美国《纽约时报》也相继报道.从1984年至1989年,就 发表了 1300多篇相关研究论文,对于Karmarkar的投影内点算法,研究者发现 这个算法与经典的非线性规划中的仿射尺度算法(affine scaling method) >对数 障碍算法(logarithm barrier method)和中心方法(center method)有关联.1994 年,Nesterov和Nemirovskii的著作进一步揭示了内点算法与非线性凸规划有着 本质的联系.内点算法对求解凸规划具有突出的数值结果推动了新的凸优化模 型的发展,如半正定规划、对称锥规划等【8】.
线性规划的原始对偶内点算法的设计思想是从初始点出发,迭代点跟随中 心路径到达问题的最优点.线性优化问题的中心路径与算法基本概念和框架 如下.
考虑标准的线性优化(LP)问题及其对偶(LD)问题.根据线性优化的最优 性条件,求原问题和对偶问题的解等价于求解如下线性方程组和不等式
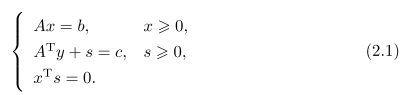
原始对偶内点算法的基本思想是通过引入参数M>0,对方程组(2.1)中的第三 个方程,即互补条件(complementarity condition),进行松弛,使其满足xTs=国 因此,考虑如下方程组
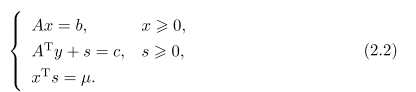
求解方程组(2.2)获得解(出夕小。)必满足冲〉0, s。> 0.显然,这些解满足内 点条件,即Ax=b,a; > 0和ATy + s=c, s > 0,且对于任意给定的/z > 0, 其解是唯一的.记该唯一解为(2;(/z),y(At),s(/z)),并称z(四)为原问题的四-中心, (g(/z),s(/z))为对偶问题的々中心.当糸趋于0时,四-中心的极限点就是问题的 最优解.
求解线性优化问题的一般原始对偶内点算法步骤如下:
(1)给定阈值参数r>0,精度参数e > 0,障碍参数0, 0 < 0 < 1;
(2)令


(3)若时


若屮(v)> t,则
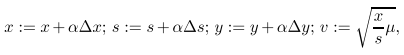 这里
这里
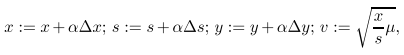 这里
这里
屮(幻是障碍函数,有不同的定义,经典的障碍函数是对数障碍函数,Peng、Kees Roos和白延琴等研究者给出了一系列障碍函数,分别命名为自正则(self-regular) 函数和核函数(kernel function),详情见文献[9].
2.4线性规划的发展方向
线性规划的奠基人Dantzig在他的文章中指出:“虽然这个世界是高度非线 性的,然而幸运的是,我们可以用线性不等式(相对等式而言)来逼近实际规划 中所遇到的大多数非线性关系.”[1]如今线性规划的理论与算法均已十分成熟,在 实际问题和生产、生活中的应用也非常广泛;线性规划问题的诞生标志着一个 新的应用数学分支一数学规划时代的到来.过去的70年中,数学规划已经 成为一门成熟的学科,其理论与方法被应用到经济、金融、军事等各个领域.数 学规划领域内,其他重要分支的很多问题是在线性规划理论与算法的基础上建 立起来的,同时也是利用线性规划的理论来解决和处理的.由此可见,线性规划 问题在整个数学规划和应用数学领域中占有重要地位.因此,研究单纯形法的 产生与发展对于认识整个数学规划的发展有重大意义.故我们有理由相信线性 规划在当今的大数据、云计算、机器学习、深度学习、人工智能、互联网时代依 然能从理论、技术以及应用方面取得突破,其依然是基础的、必要的和重要的解 决问题的炙手可热的优化工具.以下列举几个研究的重要方向和发展趋势.
(1)线性规划在整数规划中的应用.整数规划是指规划中的变量(全部或部 分)限制为整数,若在线性模型中,变量限制为整数,则称为整数线性规划.目前 所流行的求解整数规划的方法往往只适用于整数线性规划.整数规划是从1958 年由R. E. Gomory提出割平面法之后形成独立分支的,60多年来发展出很多 方法解决各种问题,现今比较成功又流行的算法是分支定界算法和割平面算法. 整数线性规划的松弛问题就是线性规划,因此,求解整数规划的方法基本依赖于 线性规划的发展.在当今的大数据、云计算、机器学习、深度学习、人工智能、 互联网时代,众多的应用问题的变量都是离散的,描述这些问题的数学或者优 化模型都是整数规划,线性规划理论算法及其应用的发展直接推动整数规划的 发展.
(2)线性规划在人工智能中的应用.2018世界人工智能大会在上海拉开帷 幕,大会以“人工智能赋能新时代”为主题.国家领导人在致2018世界人工智 能大会的贺信中指出,“新一代人工智能正在全球范围内蓬勃兴起,为经济社会 发展注入了新动能,正在深刻改变人们的生产生活方式.把握好这一发展机遇, 处理好人工智能在法律、安全、就业、道德伦理和政府治理等方面提出的新课 题,需要各国深化合作、共同探讨.中国愿在人工智能领域与各国共推发展、共 护安全、共享成果”.①事实上,人工智能的概念很宽,种类也很多.通常,按照水 平高低,人工智能可以分成三大类:弱人工智能、强人工智能和超人工智能.B 前发展比较好的是弱人工智能(artificial narrow intelligence, ANI).弱人工智能 的核心就是算法、计算力与应用场景.而线性最优化的起源就是单纯形法的强 大计算能力和战争存亡的应用场景,因此,在人工智能发展进程中,线性最优化
① 习近平致2018世界人工智能大会的贺信.www.xinhuanet.com/politics/leaders/2018- 09/17/c_1123441849.htm.
理论与技术一定是人工知识表达和大数据驱动的知识学习技术的核心基础.
(3)线性规划在机器学习的应用.众所周知,机器学习理论主要是设计和分 析一些让计算机可以自动“学习”的算法,这些算法可以从数据中自动分析获得 规律,并利用规律对未知数据进行预测,并可用于发现数据之间隐藏的关系,解 释某些现象发生的原因.因此,机器学习研究领域的众多模型与算法重点是最优 化方法,如支持向量机模型与算法、距离度量学习模型与算法、卷积神经网络等 算法.从广义上讲,机器学习算法的本质是优化问题求解,例如,梯度下降法、牛 顿法、共貌梯度法都是常见的机器学习算法优化方法.线性最优化是所有这些 算法的基础.
(4)近来关于区块链的研究兴起,区块链可以看作是分布式的数据、算力、 算法的资源集合体,所以“区块链+AI”被看作是一种解决传统AI难题的良药. 我们相信线性规划将来在区块链与人工智能数据与算法方面有极大的优势.
(5)大规模稀疏线性规划问题.关于大规模稀疏优化问题,早在1989年袁亚 湘在文章《非线性规划一现状与进展》中就给出了准确预测.他指出未来非 线性规划将在大规模稀疏问题会有重要应用【10】.从当今大数据、人工智能的应 用问题遇到的系统推荐、图像处理、模式识别等具体问题,验证了早年的预测是 非常准确的.在未来,在大数据时代大规模稀疏应用问题成为数学优化及其分 支线性规划研究的主要对象.
(6)线性规划在最优传输中的应用.最优传输(optimal transport)问题研究 的是分布之间的变换,在数学界被长期广泛关注,已经发展成为一个独立的数学 分支,并且有多位菲尔兹奖获得者在最优传输理论上做了重要研究,如A. Figalli (2018年)、C. Villani(2010年)、丘成桐(1982年).最优传输问题最早由数学家 Monge在1781年提出,但是原始的Monge问题是非凸优化问题,并且解的存 在性不一定能够得到保证.而数学家Kantorovich将Monge问题松弛为线性 规划问题,使得最优传输蓬勃发展.另外重要的_点,最优传输问题可以定义重 要的Wasserstein距离,而最优传输问题的求解决定了 Wasserstein距离的求解. 最优传输问题被广泛应用于机器学习、计算机图形学等应用领域,尤其是W- GAN模型的出现,再次使得与Wasserstein距离密切相关的最优传输问题被大 家关注.但是随着所涉及应用问题规模的增大,最优传输问题的计算再次引起 重视EL除了针对线性规划的求解算法外,梯度下降法、随机梯度下降法、加速 梯度下降法以及PDE数值求解算法逐步被用来求解最优传输问题,其中嫡正则 方法(或者Sinkhorn方法)是一个典型高效的最优传输求解算法【啊.除此之外, 感兴趣的读者可以参考关于最优传输问题的相关书籍,系统理解最优传输问题 以及线性规划的应用S’14].
(7)线性规划在深度学习中的应用.深度学习(deep learning)是一种特征 学习方法,把原始数据通过一些简单的但是非线性的模型转变成更高层次的、 更加抽象的表达.通过足够多的转换的组合,非常复杂的函数也可以被学习.深 度学习被定义为在以下四个基本网络框架中拥有大量参数和层的神经网络:无 监督预训练网络(unsupervised pre-trained network) > 卷积神经网络(convolutional neural network) > 循环神经网络(recurrent neural network) > 递归神经网络 (recursive neural network). 2006年,加拿大多伦多大学教授,机器学习领域的泰 斗Hinton和他的学生Salakhutdinov在《科学》上发表了一篇题为Reducing the dimensionality of data with neural networks的论文,开启了深度学习在学术界和 工业界研究的浪潮I*】.近年来,已经掀起了一股深度学习的巨大兴趣研究热潮. 当前多数分类、回归等学习方法为浅层结构算法,其局限性在于在有限样本和 计算单元情况下对复杂函数的表示能力有限,针对复杂分类问题其泛化能力受 到一定制约.深度学习可通过学习一种深层非线性网络结构,实现复杂函数逼 近,表征输入数据分布式表示,并展现了强大的从少数样本集中学习数据集本质 特征的能力.深度学习的实质,是通过构建具有很多隐层的机器学习模型和海 量的训练数据,来学习更有用的特征,从而最终提高分类或预测的准确性.因此, “深度模型”是手段,“特征学习”是目的.区别于传统的浅层学习,深度学习的 不同在于:①强调了模型结构的深度,通常有5层、6层,甚至10多层的隐层 节点;②明确突出了特征学习的重要性,也就是说,通过逐层特征变换,将样本 在原空间的特征表示变换到一个新特征空间,从而使分类或预测更加容易.与 人工规则构造特征的方法相比,利用大数据来学习特征,更能够刻画数据的丰富 内在信息.同时,在深度学习模型结构中,关于深度的探讨,比如多层的隐层节 点,以及数据特征的学习,各种子问题的统计与优化模型中,对于线性规划的应 用,包括局部线性化、最优性条件的线性化逼近,都是本质的和必要的.
如下的方向是比较简略的与优化领域相关的研究方向.
(1)线性规划问题并行算法设计.比如,单纯形法与内点算法混合.
(2)寻求对于一般线性规划问题或某些特殊线性规划问题的强多项式算法.
(3)求解大规模线性规划问题的一阶算法.
(4)线性规划问题算法收敛性与计算复杂性分析研究.
(5)线性规划在统计优化的应用.
(6)软件开发.
随着时代的发展,我们相信,新一代线性优化方法与技术不但以更高水平提 升整体优化方法与技术的发展,而且会以更强大的应用能力为主要目标来融入 人们的日常生活,如智慧医疗、大数据智能、自主智能系统等.在越来越多的一些应用领域,新一代线性优化方法与技术正在引发链式突破,进而推动经济社会 从数字化、网络化向智能化加速跃进.
2.5线性锥优化
线性锥优化(linear conic optimization, LCO)是从线性优化问题扩展而来 的非线性凸优化问题.线性锥优化问题是一类凸规划问题,其目标函数是线性 函数,约束集是仿射空间和一个闭凸锥的交集.它从优化问题可行域的结构方 面来推广线性规划问题,并推广问题到非线性的情况.首先从约束条件开始,引 入欧氏空间的凸锥K,为求解非线性规划问题提供了一种新的框架.它介于 线性优化和一般的非线性优化问题之间.一般情况线性锥优化包含凸二次规划 (convex quadratic programming, CQP)问题、二次约束二次规划(quadratically constrained quadratic programming, QCQP)问题等.很多投资组合优化与风险 控制问题可以建模为线性锥优化.自1984年线性规划内点算法的诞生以来,目 前在优化领域,锥优化无论是在理论算法方面,还是实际应用方面,均达到了新 的研究高潮.
2006年国际著名优化专家,冯.诺依曼理论奖获得者,国际数学家大会一 小时报告人,国际著名优化专家美国佐治亚理工学院(Georgia Institute of Technology) A. Nemirovski在2006年西班牙举行的国际数学联盟大会的一小时报告 I!Advanced in Convex Optimization: Conic Programming,, 中总结了 20 年来优 化领域的最新进展,他指出:过去的20年中,在凸优化领域主要进展是锥优化, 即线性、锥二次优化和半正定优化.锥优化揭示了凸优化所具有的丰富结构,这 种结果能促进算法的有效性【16】.
线性锥优化具有像线性规划一样丰富的最优性和对偶性理论.它的对偶问 题和原问题具有结构与代数上的对称性.进一步,线性锥优化问题有非常广泛的 应用背景,除了在传统学科,如投资组合风险管理、无线信号定位、工业设计、最 优控制等经典问题,还在新兴学科有广泛的交叉应用,如稀疏优化、人工智能、 大数据、云计算、信息和网络技术等.20世纪80年代兴起的内点算法发展和丰 富了线性规划的求解方法以及计算复杂性分析,也成为求解线性锥优化问题的 强大工作.迄今,线性锥优化和内点算法已成为数学优化领域最活跃的研究领域 之一.线性锥优化主要包含三类重要的优化问题:线性规划、二阶锥规划和半正 定规划问题.其中,半正定规划的应用非常广泛,在组合优化及图论中都有很好 的应用,如图论中的最大割问题、球的镶嵌问题等均可用半正定规划将NP-难问 题转化成凸的可计算问题IM.有兴趣的读者请参考比较经典的文献[18]和[19], 线性锥优化问题的数学模型如下:
(LCO) min(cTa:: Ax — be XS},
这里A e Rmxn, beRm和c 晔.目标函数是cTx,决策向量是2;eRn, Ax-b 是从R”到Rm的仿射函数http://academics.casad.cas.cn/xkfz/sxyh/202101/C是Rm闭凸点锥.这类问题的重要性体现在如 下两方面.一方面,很多优化问题可以表示成锥优化形式.另一方面,若锥满 足适当的假设,则此类问题可由有效算法求解.
锥K,的一个最简单的例子是m维欧氏空间的第一象限锥,即兀=畔. 因此,锥优化是线性优化问题的推广.三种常见的闭凸点锥是第一象限锥、二阶 锥(second-order cone, or Lorentz, or ice-cream cone)和矩阵空间的对称半正定矩阵锥,其定义如下:
(1)第一象限锥:

⑵二阶锥:
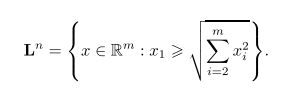
(3)对称半正定矩阵锥:

2.6线性锥优化对偶理论
一个凸锥的对偶锥定义如下:

2.5节提到的三种锥都是对称锥,即锥和它的对偶锥相同,亦称为自对偶锥.同 时,它们还是齐次锥更为广泛的锥可表示为这三类锥的有限卡氏积.关于凸锥 和它的对偶锥理论,读者可参考文献[20],
(LCO)问题的对偶问题是
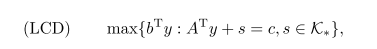
其中,/C*是/C的对偶锥.如下分别给出二阶锥优化问题和半正定优化问题以及 它们的对偶问题.
二阶锥优化问题及其对偶问题:二阶锥优化问题的标准形式
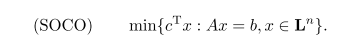
它的对偶问题是

其中,LCR"是几个二阶锥的卡氏积,即
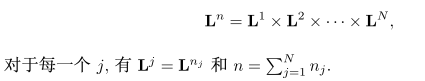
半正定优化问题及其对偶问题:半正定优化问题的标准形式

其对偶问题是

其中,
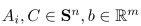 不失一般性,总是假设矩阵At线性无关.
不失一般性,总是假设矩阵At线性无关.
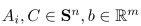 不失一般性,总是假设矩阵At线性无关.
不失一般性,总是假设矩阵At线性无关.
关于锥优化的对偶定理有几种表示,这里为了和线性优化的对偶理论表示 一致,我们简略描述了对偶定理,详细的理论可以参考文献[20].
(1)弱对偶定理:对于任意原问题的可行解灯(或X)和对偶问题的可行解 y,恒有 C& 2 bTy.
(2)如果原问题严格可行且有下界,则对偶问题可解.
(3)如果对偶问题严格可行且有上界,则原问题可解.
(4)强对偶定理:如果原问题与对偶问题都有界且严格可行,则芥是原问 题最优解且0*为对偶问题的最优解:
当且仅当尸"=任炉(零对偶间隙).
当且仅当(C - 4切*)&*=0 (互补松弛).
2.7线性锥优化的求解方法
2.7.1内点算法
求解线性锥优化问题的内点算法的思想如下:
首先,在给定的可行域K内构造一个光滑且严格凸的内罚函数(障碍函数) F(时,考虑如下参数化的优化问题
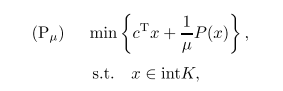
这里 > 0是参数.
其次,在合适的假设下,对于每一个/z>0,问题(PM)有一个唯一的解勿*3), 这个解在锥K的内部.
参数化的优化问题(PM)形成一个连续路径芥(小,M e (0,+8),并当〃- +0O时,收敛到原问题的最优解.
由此原问题可行域的中心路径(central path)是

求解线性锥优化问题的内点算法的路径跟踪策略是:
(1)内罚的算法框架把原问题转化成一系列无约束优化问题(PM).
(2)中心路径产生迭代点列S,如并跟踪了梦3),使得当W T +8时,有 Xi -灯*(同)—> 0,其中 Hi —> +oo.
(3)当迭代点 国如 是 W) 一个好的近似时,校正队到出+1,极小化 电+1(勿),开始新一轮迭代xi+i,它是a:*(巨+1)的近似
2.7.2其他方法
香港理工大学孙德锋教授在20世纪90年代中后期发展了半光滑和光滑化 牛顿方法,开辟了矩阵优化这一新的学科领域,建立了非光滑矩阵分析,在矩阵 优化的理论、算法及应用方面取得了一系列奠基性的成果,提供了求解线性锥 优化的方法,主要参考文献[21],
北京大学文再文教授与合作者基于ADMM (alternating direction method of multipliers)与 DRS (Douglas-Rachford splitting)的等价性,发展了一种二阶型 方法,把SDP作为一个非线性方程组进行重新计算,并提出了一种自适应半光 滑牛顿方法,证明了该算法可以收敛到全局最优解.在某些假设下,这个二阶型 算法能够实现超线性或二次收敛.数值结果表明,该算法可以比现有的最佳算 法SDPNAL更快地达到相当的精度,主要参考文献[22],
2.8线性锥优化发展方向
由于线性锥优化问题有非常广泛的应用背景,它又具有像线性优化问题同 样多的优点,如简单的最优性条件和丰富的对偶性理论.对复杂应用问题的描述 性,以及有效的求解方法,因此,关于线性锥优化的研究前景非常广泛.如下列 举几方面的发展思路与前沿方向.由于作者的知识局限性,仅供读者参考.
(1)非对称锥优化的具有多项式时间近似算法研究:线性锥优化根据约束锥 的自对偶性和非自对偶性分为两类:对称锥优化和非对称锥优化模型.对称锥优 化模型目标函数是决策变量的线性函数,约束集是自对偶的齐次(homogeneous) 凸锥与仿射空间的交集.这类优化模型主要是线性规划、二阶锥优化和半正定 锥优化模型.由于约束锥具有对称性,这类锥称为可计算锥,对应的优化问题 可用具有多项式时间的内点算法求解.然而美国康奈尔大学数学与运筹学专家 Renegar 教授在他的著作 A mathematical view of interior-point methods in convex optimization中指出在向量空间和矩阵空间对称凸锥仅有五类,其中三类是常见 的n维欧氏空间的第一卦限锥、二阶锥和半正定矩阵锥、余下的两类目前没有 用以优化建模.因此大部分凸锥是非对称锥.
非对称锥优化模型,顾名思义,是指约束锥是非自对偶的凸锥与仿射空间的 交集,其目标函数是决策变量的线性函数.这类锥优化模型的突出优点表现在三 个方面:第一方面是,对于非凸二次规划问题(连续或者离散)或者是组合优化 NP-难问题可用非对称锥吸收、隐藏和描述非凸性和NP-难的,把这两类问题等 价转化成凸锥优化问题.第二方面是,当非凸问题不能进行等价转化时,为这些 问题建立锥松弛,能够得到比对称锥(半正定锥)更紧的界.因此非对称锥优化模 型成为处理非凸二次规划和组合优化NP-难问题的有力工具.第三方面是,非对 称锥优化模型被广泛应用于机器学习、分类问题、鲁棒优化、投资组合优化、博弈 与均衡,以及图像处理等实际问题的建模与计算.然而,虽然非对称锥优化在形 式上保存了对称锥优化问题的特点,但在设计算法方面和对称锥优化问题有三 个本质的差别,具体表现在:首先,决策变量有时没有显式表达,比如对于完全正 锥(completely positive cone)元素就是借用集合的凸组合表达的.因此对于优化 问题的决策变量可能由向量和矩阵混合表示或者是矩阵不等式表示,其中参数 不明确.这种表示导致维数巨大、计算难度与成本都大等问题.其次,原始问题和 对偶问题的对偶间隙存在性问题.最后,最重要差别还是在约束锥上,当约束锥 是非自对偶锥时,直接导致了验证决策变量是否属于非自对偶锥就是NP-难问 题.比如,当约束锥是协正锥(conpositive cone)或者是它的对偶锥完全正锥,验 证一个变量是否属于协正锥或者完全正锥是NP-完全问题.因此,非对称锥优化 的理论与近似算法成为国际优化领域研究的热点.2012年Bomze等给出协正锥 的进展和应用【23】.同年国际数学优化学会(National Mathematical Optimization Society)在其会刊(Mathematical Optimization Society Newsletter)指出 了优化 领域的热点课题,刊登由Bomze, Diir等的综述文章Copositive optimization,并 提出了公开问题:如何设计求解具有简单锥结构非对称锥优化问题的多项式时 间的算法.北卡罗来纳州立大学方述诚教授与清华大学的邢文训教授的著作也 对非对称锥优化的理论与算法做了深刻研究【24].这些信息均表明了研究非对称 锥优化理论与算法是锥优化的重要研究方向之一.
(2)内点算法计算复杂性分析研究:内点算法是求解线性优化问题、线性锥 优化以及相关问题强有力的工具.在应用方面,基于内罚函数的原始对偶内点 算法是各种内点算法中最简单与实用的方法.理论上,这个方法的计算复杂性 非常好.基于内罚函数的原始对偶内点算法有大步方法(large-update method) 和小步方法(small-update method)之分.在实际数值应用中,大步方法比小步 方法效果好,然而在计算复杂性分析上,小步方法的计算复杂性好.它们的计算 复杂性分别为0 (nlog (:))和O (闿log Q),这里n是问题决策变量的维 数,两者的差距(gap)与因子而同阶,当n很大时,差距非常大.因此,解决大 步方法和小步方法理论计算复杂性差距是一个重要的研究课题.
(3)非线性锥优化的理论与算法研究:大连理工大学张立卫教授[2句领衔的 团队和香港理工大学孙德锋教授【26】在非线性锥优化理论,包括矩阵优化理论等 方面均有突出的研究工作.由于非线性锥优化的最优性条件非常复杂,因此研究 开发求解非线性锥优化的有效算法将是一个研究方向.
(4)线性锥优化在机器学习问题的松弛模型研究:线性锥优化具有特殊描述 优化问题可行域结构的性质,因此具有强大的描述现实复杂问题的能力,以及 模型转化能力,最终能使得优化模型具有有效的近似算法.比如距离度量学习 中的决策变量的可行域是对称正定矩阵黎曼流形.它的数学模型是非常复杂的, 是没有多项式时间计算的模型.通过建立合适的线性锥优化松弛问题,研究原 问题与松弛问题之间的等价以及误差界的关系、最优解的关系等,为解决机器 学习问题提供研究方法.
(5)锥优化软件平台开发:求解半正定规划的第一个软件是来自荷兰的 SEDUMI,后来由加拿大MK Master大学的优化团队维护.随着时代的变迁, 对求解线性锥优化的软件开发更是迫切.关于这方面的工作,新加坡国立大学的 研究团队在线性锥优化、矩阵优化的软件开发与平台建设已经做了非常重要的 工作則.北京大学文再文教授以及合作者也开发了软件,参见文献[22].
(6)线性锥优化在人工智能等领域的应用研究:因为对于一般情况,人工智 能解决问题的方法最终需转化成优化模型或者统计模型.这些问题具有复杂的 目标函数或者约束条件,这些问题与锥优化模型之间的转化是重要的途径之一.
(7)锥优化与矩阵优化的相关研究:矩阵优化问题(matrix optimization problem) 是指目标函数或约束函数中含有矩阵变量的优化问题.这类问题大量出现 在图像处理、推荐系统、机器学习、稀疏优化、数据挖掘、高维统计等领域,在 当今大数据、人工智能和深度学习有着广泛的应用,矩阵优化已经成为最优化 领域一类重要的优化问题[27】.比如,矩阵秩优化问题和低秩矩阵分解问题都是 典型的矩阵优化问题.由于许多矩阵优化问题是非凸的、非光滑的,甚至是不连 续问题,大部分是NP-难问题,所以研究求解矩阵优化问题的高效算法是非常必 要的.矩阵优化与锥优化有着非常密切的关系,比如,半正定优化问题就是矩阵 优化的特例.因此矩阵优化问题的锥松弛模型、近似算法、误差界等是研究矩 阵优化问题的重要途径之一.
(8)锥优化与张量优化的相关研究:张量是向量和矩阵的高阶推广.最近十 几年来,张量优化的理论与应用研究得到迅速发展.其中一类重要问题是张量锥 规划问题,例如,完全正张量锥规划问题、非负张量锥规划问题等.很多NP-难 问题都可以等价转化为完全正张量规划问题.例如,混合0-1二次规划问题、图 的近似稳定数等.特别地,Pena等于2015年在较弱的条件下,证明了一般的 多项式优化问题均可等价转化为完全正张量规划问题【28].但是由于张量锥本身 结构的复杂性,关于一般张量锥规划的有效全局求解算法仍是一个重要的研究 课题.
(9)随机线性(锥)规划.随着随机优化算法在机器学习中分布式和随机优 化领域获得广泛的应用,比如随机梯度算法在解决大规模计算和去中心化问题 上显示出优势.这些发展可以推动线性锥规划从确定性模型发展到随机化模型 或者是分布式将成为一种趋势.


 上一篇
上一篇 



