正好两门课都上过,两门课的侧重点还是不一样的。
运筹学着重于解决实际问题,能看到运筹学上的例子都是有实际背景的,而相应的理论也是由于对应的问题出现而出现的。如运输问题,图与网络问题,排队论,存储论,对策论等等。
最优化侧重于各种最优化问题的算法,特别是算法的收敛性和收敛速度。往往一个问题有多种算法。如一维搜索,导数法(最速下降法,牛顿法,最小二乘法等等),无约束最优化的方法,可行方向法,二次规划的拉格朗日法等等。
当然两门课都有一些共同点。比如都从线性规划和凸规划开始,介绍单纯形法,对偶问题,灵敏度和运输问题,整数规划等等。
运筹学的目标就是优化
二者唇齿相依,唇寒齿亡。
最优化是数学里面的一个领域,就是求一个函数在它的定义域里面的最优值。函数是给定的,只关注于怎么解。
运筹学是管理学里面的一个领域,关注的是管理里面的定量问题和管理中能通过数学建模得到洞见的问题。不仅关注怎么解决这个问题,更重要的是从现实中找出问题,然后定义成数学问题。
如果没有最优化,定义了问题不知道怎么解也白定义。如果没有运筹学,连问题都没有,最优化就是没事找事干,解出来也没有实用价值。
最优化说到底只是工具,不过它是数学工具罢了。定义好问题,如果正好是经典的运筹学里面的问题,例如线性规划,二次规划,某些图论问题,某些调配问题,某些整数规划等,大多数问题都已经有软件可以直接解,不愿意学数学的人也可以通过软件解决问题。关键是模型见得合理而且正好套得上现有的模型。
如果模型不是现有的标准模型,就要用其它数学工具去解。那些问题可以留给研究者,或者你自己学些数学工具去解决。
如果只关注运筹学,可以直接先学每一章的建模部分,了解这类模型能解决什么问题,然后在看看是不是多项式时间可以解决的问题,所谓P问题(就是那些可以用软件解的问题),如果是,记下用什么软件解,下次用到查一下就直接解,如果不是,以后建模尽量不要建这种。
如果只关注最优化,直接拿起书看目录,看看都有什么内容,看每一章是解一个长什么样的函数,就知道了以后能解决什么问题。然后再逐章学,一般前一章会是后面的基础,不好跳。
当然,如果两样都会,那就最好了。
不是一回事,最优化是一种数学方法,本质上是求方程数值解的一种技术,像第一性原理、有限元、蒙特卡洛、分子力学甚至人工智能上都在用各种优化算法,运筹学主要还是要辅助决策,只是其中大量在使用最优化方法。
- 奇异博士脑子里一定有一个运筹优化求解器
- 建模和优化求解两回事
- 任何人工智能问题,基本都会归到优化问题
- 机器学习归到代价函数优化求解,统计学习归到极大似然函数求解
- 深度学习属于极度非凸无约束优化问题
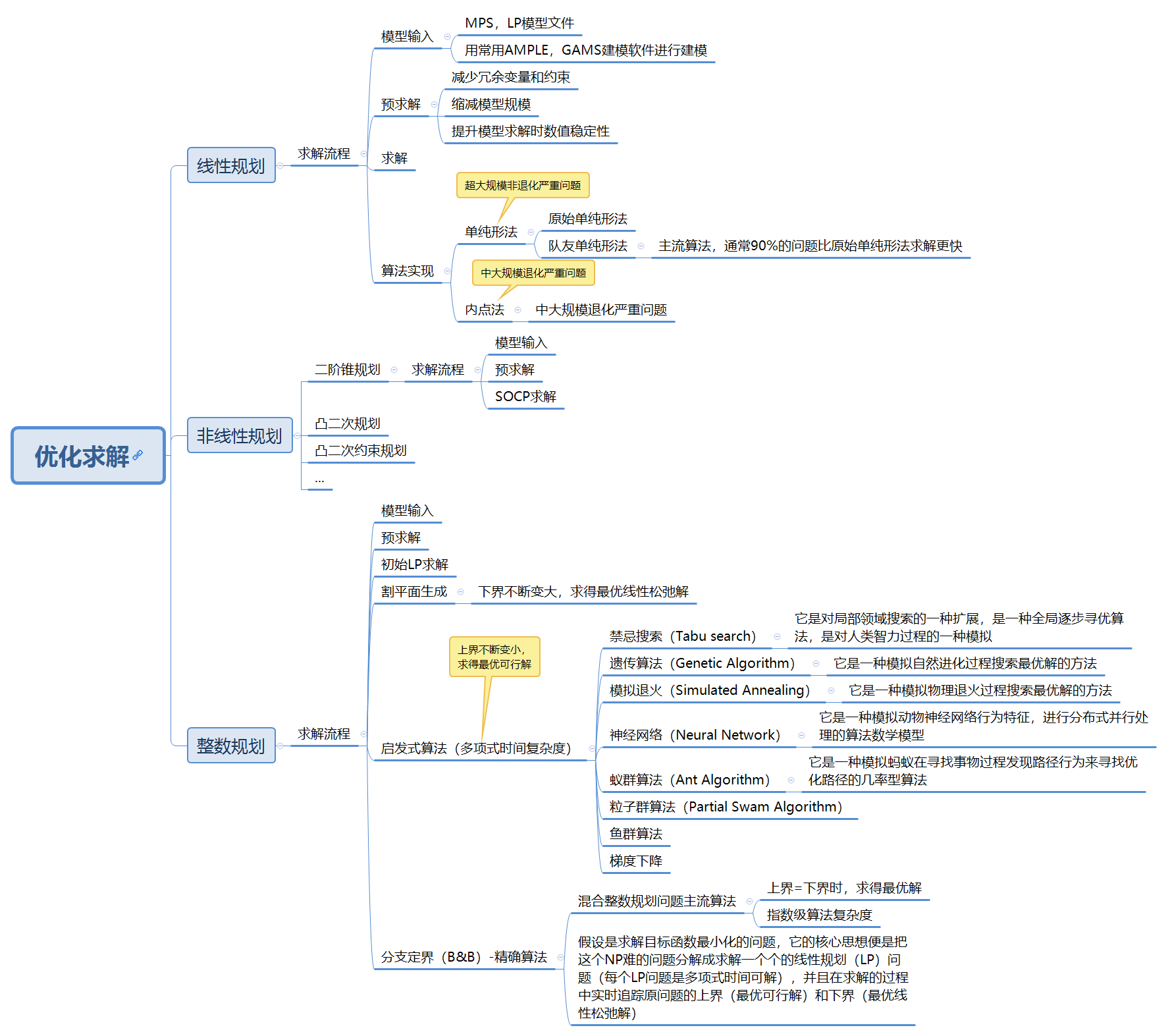
- 优化求解大概包括精确求解和近似求解,精确求解催生优化求解器,近似求解获得近似解(理论可证),启发式求解获得局部最优解(没有任何保证的局部最优解)
- 优化模型可以分为线性规划模型、非线性规划模型和混合整数规划模型
- 有模型,可以精确求解,获得理论可证的全局最优解,但是指数级算法复杂度。可以用启发式算法求得最优可行解,作为优化求解器的初始解。这时候,优化求解器只需求解Root Node(LRP),便可以得到下界,于是你几乎不费力(多项式时间)便可得到一个Gap。这个Gap,便可以作为这个解的某种保证(例如,Gap是10%,你便知道这个解离最优解“不远了”)
奇异博士脑子里一定有一个运筹优化求解器,不信你看下面这个视频。
它主要研究人类对各种资源的运用及筹划,在满足一定约束的条件下,以期发挥有限资源的最大效益,达到总体最优的目标。它的几个“别名”:数学规划 (math programming)、优化 (optimization)、最优化理论、决策科学(Decision Science)等。专业:数学系运筹学专业、计算机学院理论计算机专业等。主要以下几方面应用:
- 供应链(Supply chain)
- 路径优化(Routing Problem)
- 仓储、运输等物流(Logistics)
- 生产流程优化(Process Optimization)
- 电子工程里的设施部件分配问题(Facility Layout Problem)
- 火车、课程、飞机时刻表安排问题等调度问题 (Scheduling Problem)
- 资产配置 (Asset Allocation)、风险控制 (risk management)等经济金融领域的应用
- 有“最”字,如:利润最大化、成本最小化,基本就和运筹学息息相关
运筹优化场景中,先建模,后求解,两个事情同等重要,建模难在行业知识和经验,求解难在技术和经验。
LEAVES,上海财经大学并行优化国际合作实验室与杉数科技共同建设的一个运筹学与人工智能基础算法平台。
CMIP,中科院CMIP混合整数规划求解器。
MindOpt,达摩院决策智能实验室自主研发的数学规划求解器套件。
COPT,杉数科技工业级别整数规划求解器。
PlatEMO,安徽大学生物智能与知识发现(BIMK)研究所开发的进化多目标优化平台,开源免费的代码库,仅供教学与科研使用,不得用于商业用途。
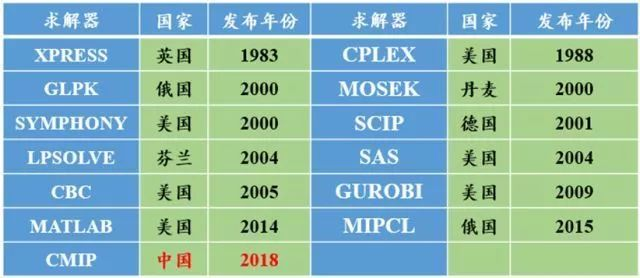
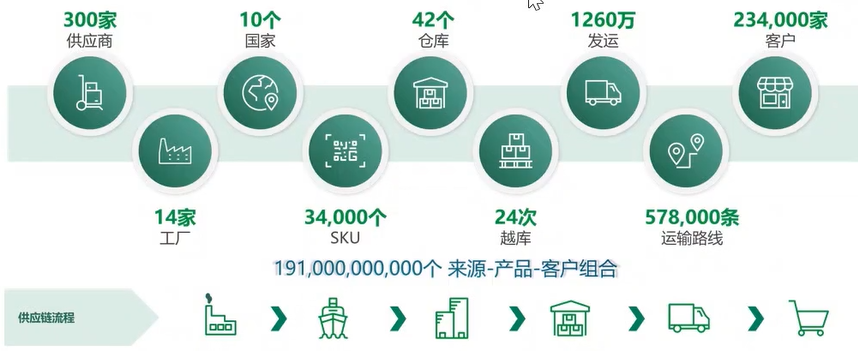
先来体验下供应链优化的复杂程度。
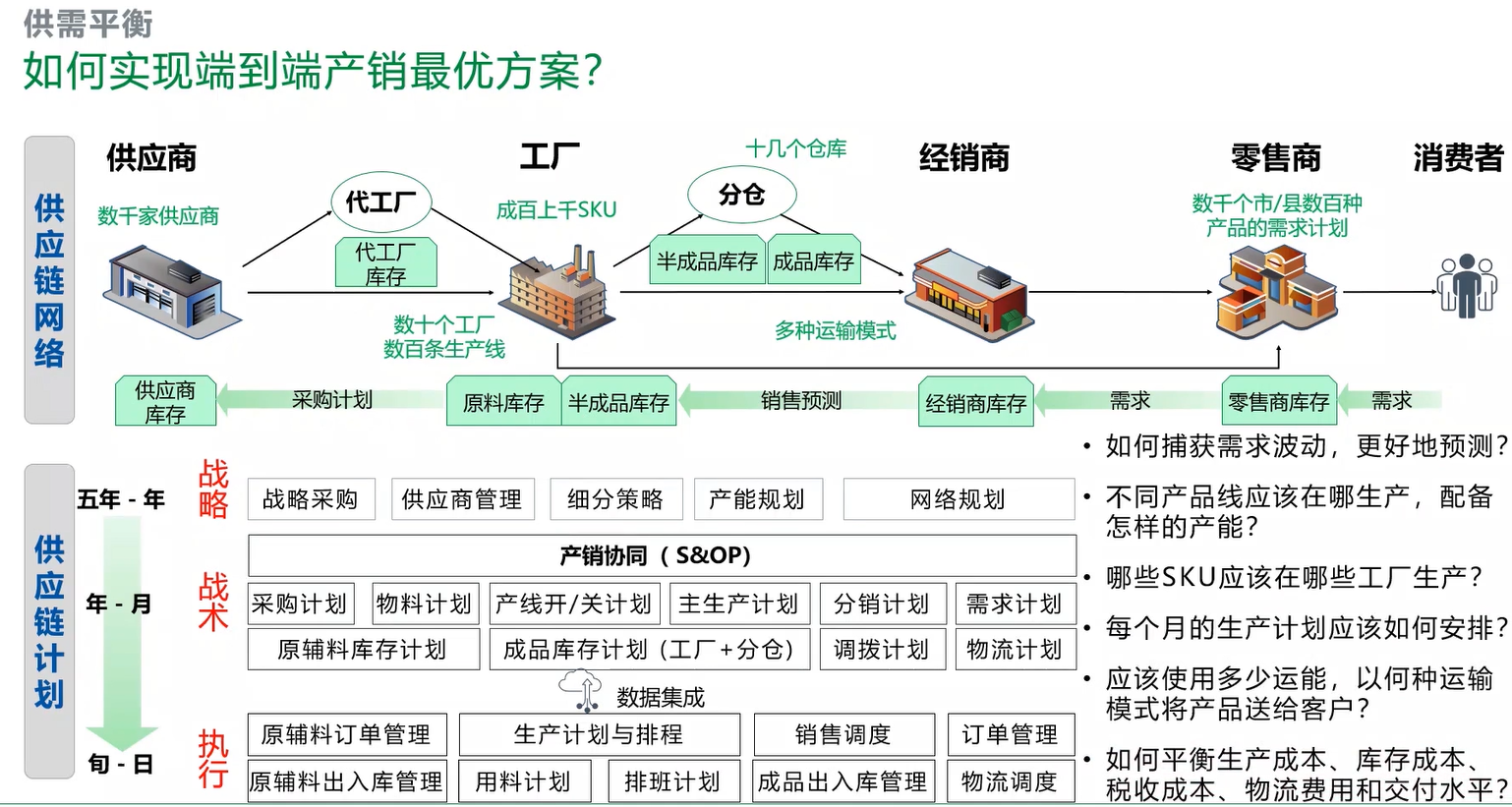
端到端的产销运筹优化。
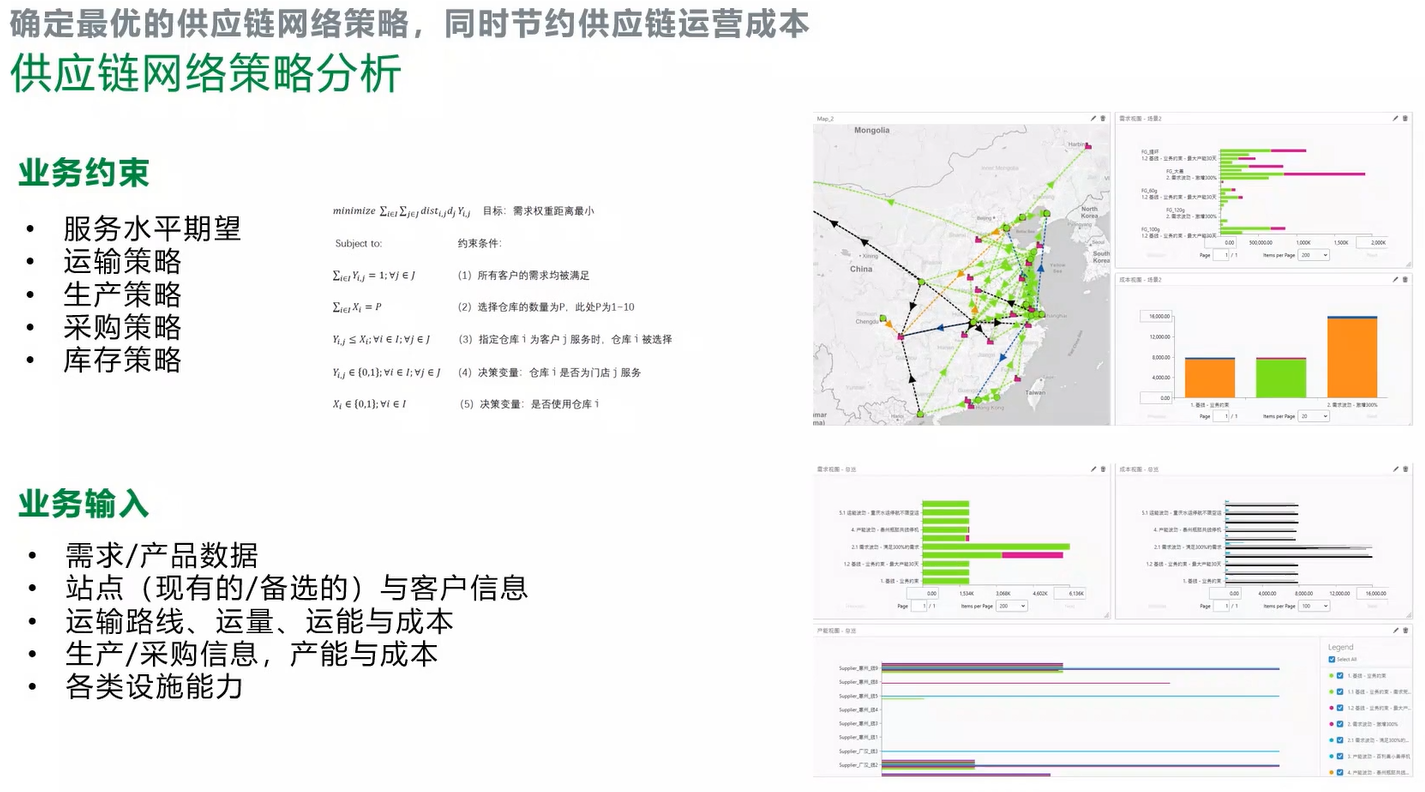
这个知道的人似乎不多,我来写一下。
PlatEMO,全称Platform for Evolutionary Multi-objective Optimization,由安徽大学BIMK(生物启发智能与挖掘知识研究所)和萨里大学NICE(自然启发计算与工程组)共同开发。已开源,用于科研,GitHub自行下载。
- 200+开源进化算法
- 400+开源benchmark问题
- 用于并行执行实验的强大 GUI
- 一键生成Excel或LaTeX表格
- 持续更新先进算法
- 完全在 MATLAB 中开发。PlatEMO 包含许多 MATLAB 函数,无需使用任何其他库。无论操作系统如何,任何能够运行 MATLAB 的机器都可以使用 PlatEMO。
- 包括许多流行的算法。PlatEMO 包括九十多个现有的流行 MOEA,包括遗传算法、差分进化、粒子群优化、模因算法、分布估计算法和基于代理模型的算法。大部分是2010年后发表在顶级期刊上的代表性算法。
- 多种图形演示。用户可以选择多种图形进行展示,包括结果的Pareto前沿、结果的Pareto集、真实的Pareto前沿以及任意性能指标值的演化轨迹。
- 强大而友好的图形用户界面。PlatEMO 提供了强大而友好的图形用户界面,用户可以通过图形用户界面配置所有设置并并行进行实验,而无需编写任何代码。
- 生成Excel或LaTeX格式的数据。用户可以将PlatEMO生成的统计实验结果保存为Excel表格或LaTeX表格,可直接用于学术写作。
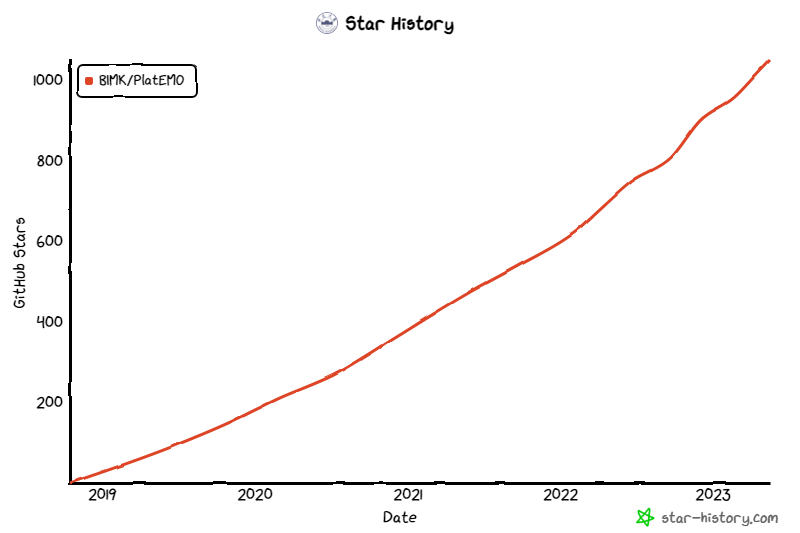
GitHub star数据还行。
哪位大哥了解,帮忙丰富一下,我就知道LLamasoft和杉数科技,知道的就回复在评论中。
祝回复的大哥大吉大利,夜夜吃鸡!
对运筹学感兴趣的人,建议关注 @留德华叫兽 ,文章里大部分知识都是引用过来的,如侵删。
Comparison of optimization software - wiki
GitHub - BIMK/PlatEMO: Evolutionary multi-objective optimization platform


 上一篇
上一篇 



