中学阶段几个超纲的巧妙结论(1)_奇亿娱乐-注册登录绿色站

项目简介

访问网站
访问手机网站

项目服务

提交需求
策划设计
技术开发
维护修改
售后服务

序-

小编我自己也是中考生(这篇文章是中考前20天写的)，在学习过程中我发现了一些书上或者资料上没有的结论，当然是相对来说比较常见的结论，不过中考或者高考肯定不会让你证(因为确实超纲了，当然要必须可以用范围内方法做，而且得常见，不然这定理有啥用/笑)

这篇文章算是个起点吧，我以后发现更多有趣的结论会写后续，主要是我也是初中生，高中的题做的不是很多，就捡最常见的特殊结论说说，毕竟这是第一期/又笑

每个定理我会给出证明，不过既然是超纲的结论，尽管可以用学过的知识解答，但我可能会用高等数学解法，请勿怪罪

这一系列文章一方面是为了启发后面的学生，另一方面我也可以对自己的发现做一个总结，也算是激励自己

建议比较熟悉中学知识的朋友们阅读，一方面是容易记错，另一方面的话解答题也不让用，用于检查或者填空题，为了避免误入歧途，不是特别建议基础差的同学看

·目录:
一.预备知识

二.初中篇
1.平行四边形和三角形面积公式拓展
2.二次函数面积最大问题

三.高中篇
1.平行六面体和三棱锥体积公式拓展
2.泰勒展开式列举

提前说过，这些定理一般的数学好的同学可以深入研究，其实第一期的内容很浅显，算是只是提醒大家还有这个公式而已吧，如果这些还是看不懂的话可以记住死结论，反正肯定是有用的。

(1) $f\\left( x \\right)$

估计不少同学见过这玩意儿，也对此好奇过，懂得的甚至拿 $f\\left( x \\right)$ 炫耀自己"学识渊博"/笑，那么这到底是个啥呢

$f$ 是 $function$ 的简写，如果你查翻译，是这个意思

仔细看， $function$ 有一个意思是"函数"，是不是豁然开朗？！那 $(x)$ 又是啥啊？

其实这个表示的就是自变量为 $x$ ，这个整体表述就是一个以 $x$ 为自变量的函数！

我们for个example
$f\\left( x \\right)=ax^2+bx+c$ 表示的就是一个二次函数，要注意的是，这里是 $f(x)$ 因此和 $a,b,c$ 是没有关系的，我们称之为参数或者参变量，你看， $f(x)$ 写起来比 $ax^2+bx+c$ 简单多了吧，注意的是你开头得交代y一下，因为关于 $x$ 的函数有无数个，鬼知道你要的哪个
注意： $f(a)是表示在已知f是x的函数，而且a和x无关时，f(x)在a的取值$

(2)向量(vector)

估计一些dalaoes看到我的目录就知道我要讲向量吧/doge

其实我们学的数或者"未知数"( $eg:1,\\pi,\ heta,x,y,z,\\sqrt4$ )都叫标量(scalar)，类似的还有向量(vector)，矩阵(matrix)，张量(tensor)，这群鬼东西不知道没事，我们只学学向量/放肆笑

我们不妨望文生义一次

向量，有方向的量咯? right!!

我们一般这样标记

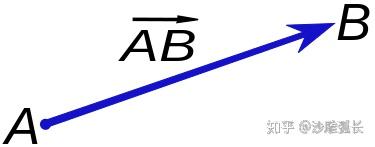
这样以A为起点B为终点的"箭头"记为 $\\vec{A B }$ (知乎的 \\vec 好丑/哭) (写成 $\\vec{a}$ 也没人说你)

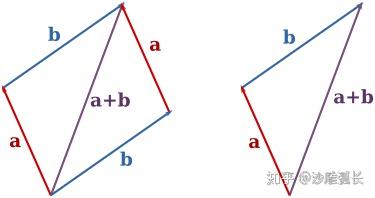
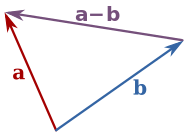
有同学要问了：向量既然也是量，那它怎么运算呢？

上图就是运算规则，如果把它理解为三角形的话就有点反常识了，这三边关系不对啊!

其实,这是没问题的，向量指的是一个路径，稍微思考，我先从A到B再到C和我从A到C当然是一样的啊,所以就有 $\\vec{AB}+\\vec{BC}=\\vec{AC}$

另外还要介绍一个东西——模

这是啥呢？我们看，向量是一个有方向的东西，但是它看起来好像有长度啊，怎么表示长度呢？其实这就是模，(也可叫范数，而且是二维的范数—— ${\\displaystyle \\|{\\boldsymbol{x}}\\|_{2}={\\sqrt{x_{1}^{2}+\\cdots +x_{n}^{2}}}}$ ）细心点看，ahhhhhh，其实就是长度!

我们还得分析，这玩意儿咋表示呢，你 $\\vec{a}$ 也看不出来长啥样啊，

我们把平面直角坐标系搬出来，

如图，A(a1,a2)，B(b1,b2)，则vector(AB)=(b1-a1,b2-a2)

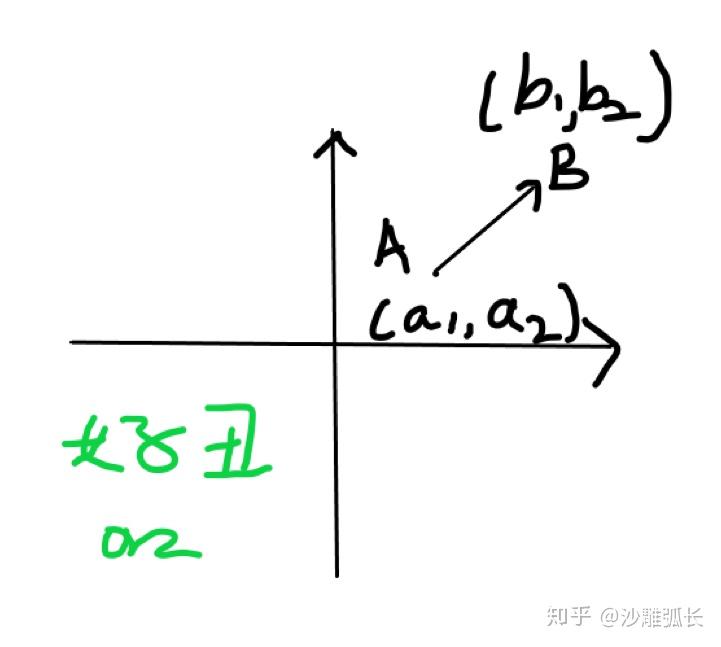
如图 $A(a_1,a_2),B(b_1,b_2),\\vec{AB}=(b_1-a_1,b_2-a_2)=(\\Delta x,\\Delta y)$ ，大功告成！

向量还有乘法，includes 数量积和向量积，我这里不展开，主要就是

${\\displaystyle{\\vec{a}}\\cdot{\\vec{b}}=\\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\\cdots +a_{n}b_{n}}=||a||||b||cos(\ heta)[\ heta为\\vec{a}和\\vec{b}夹角]$ (点乘，数量积)

${\\displaystyle ||\\mathbf{a}\ imes \\mathbf{b}||=\\|\\mathbf{a}||\\|\\mathbf{b}\\|\\sin(\ heta )\\ }$ （ $\ heta为\\vec{a}和\\vec{b}夹角$ ）（叉乘，向量积)

——————我是分割线——————

1.平行四边形和三角形面积公式拓展

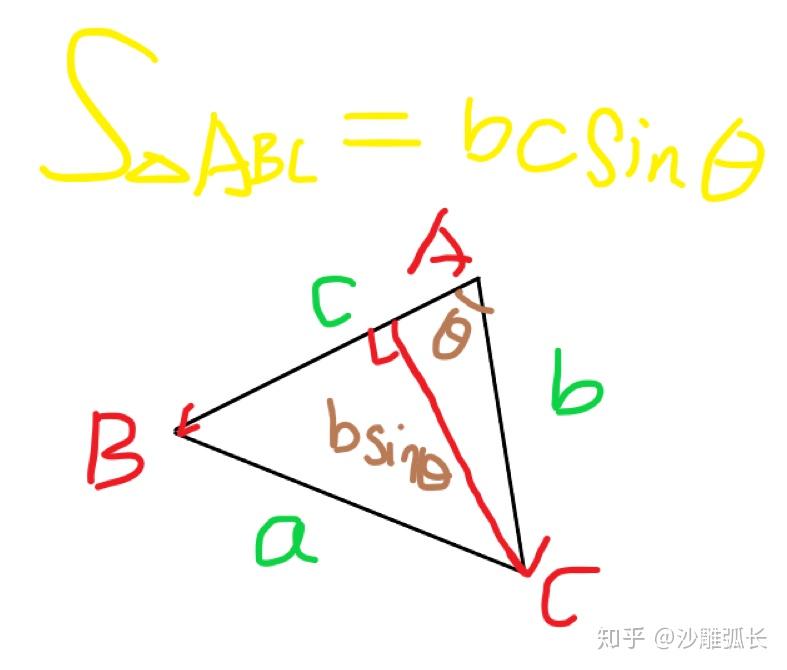
上文提到 ${\\displaystyle ||\\mathbf{a}\ imes \\mathbf{b}||=\\|\\mathbf{a}||\\|\\mathbf{b}\\|\\sin(\ heta )\\ }$

完美贴合！这时候我们直接用 $\\vec{a}×\\vec{b}$ 的另一种形式(留了一手/笑)

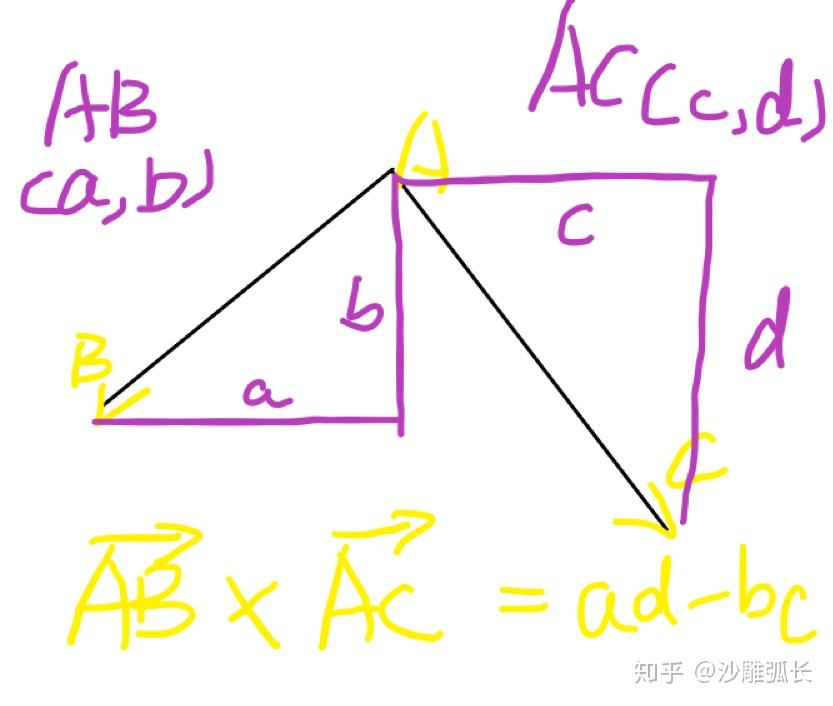
显然，面积公式就是 $S=\\frac{1}{2}|ad-bc|$

小练习：
在平面直角坐标系中，求 $A(1,2),B(7,5),C(6,6)$ 为顶点的三角形面积

2.二次函数面积最大问题

定理一 : 已知二次函数中有俩点 $A(m,f(m)),B(n,f(n))$ 且为定点 ,其中 $f(x)=ax^2+bx+c$ ，有一点 $C(c,f(c))$ 也在抛物线上，当 $S_{\\Delta ABC}$ 最大时， $c=\\frac{m+n}{2}$ 即AB横坐标的一半。

证明这玩意儿，我们得证明一个引理

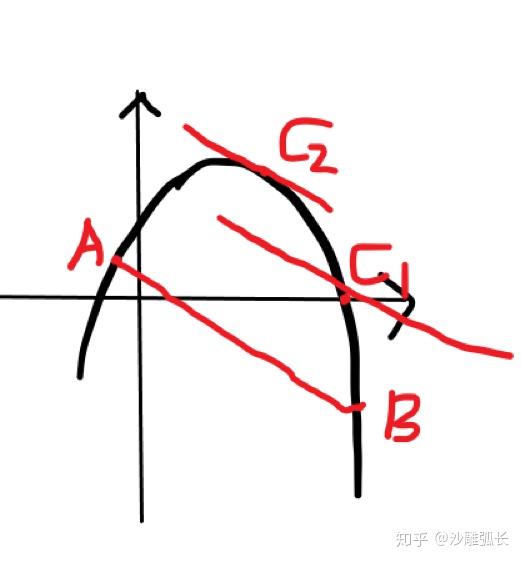
看这个lovely二次函数，你会发现过C做AB的平行线，和二次函数图象相切时面积最大(这是引理？表述太不严谨了吧)

过 $C$ 做 $CD||AB$ ，和二次函数另一交点为 $D$ ，当CD重合时 $S_{\\Delta ABC}$ 面积最大
证明：
观察法，易证，不写，证毕.

CD重合时是啥情况嘞？我们这样想：二次函数和x轴只有一个交点的时候是不是就AB重合了？那不就是 $f(x)=0$ 且,判别式 $\\Delta=b^2-4ac=0$ 吗？

借此，我们来证明定理一：

把AB向平移k个单位，由于最初AB解析式带进去得到 $f_{AB}=\\frac{f(m)-f(n)}{m-n}x+(f(m)-\\frac{f(m)-f(n)}{m-n}m)$ ，其实没必要这么麻烦，我们直接假设A在y轴，这样也不影响，变成 $f_{AB}=-\\frac{f(m)-f(n)}{n}x+f(m)$ ,平移之后 $f_{CD}=-\\frac{f(m)-f(n)}{n}x+f(m)+k$ ，然后我们求交点坐标就是联立它和二次函数 $-\\frac{f(m)-f(n)}{n}x+f(m)+k=f(x)$ ，带入 $f(x)=ax^2+bx+c$ 令 $\\Delta=0$ 解出 $k$ 然后带回原式即可求C横坐标 $=\\frac{m+n}{2}$

这玩意儿也忒复杂了吧，有没有什么方法呢？

这里提出一个自创方法，可能不严谨吼

由lagrange中值定理： $f'(\\xi)=\\frac{f(m)-f(n)}{m-n}=\\frac{am^2+bm+c-an^2-bn-c}{m-n}=\\frac{a(m+n)(m-n)+b(m-n)}{m-n}=am+an+b$ 又 $f'(\\xi)=2a\\xi+b$ ,所以 $\\xi=\\frac{m+n}{2}$ ,证毕!

hu lalalalala~(赶紧翻开资料算算吧！)

对于评论区中dalao @霜夏的方法我用GGB画了一个图方便大家看再次感谢dalao提醒

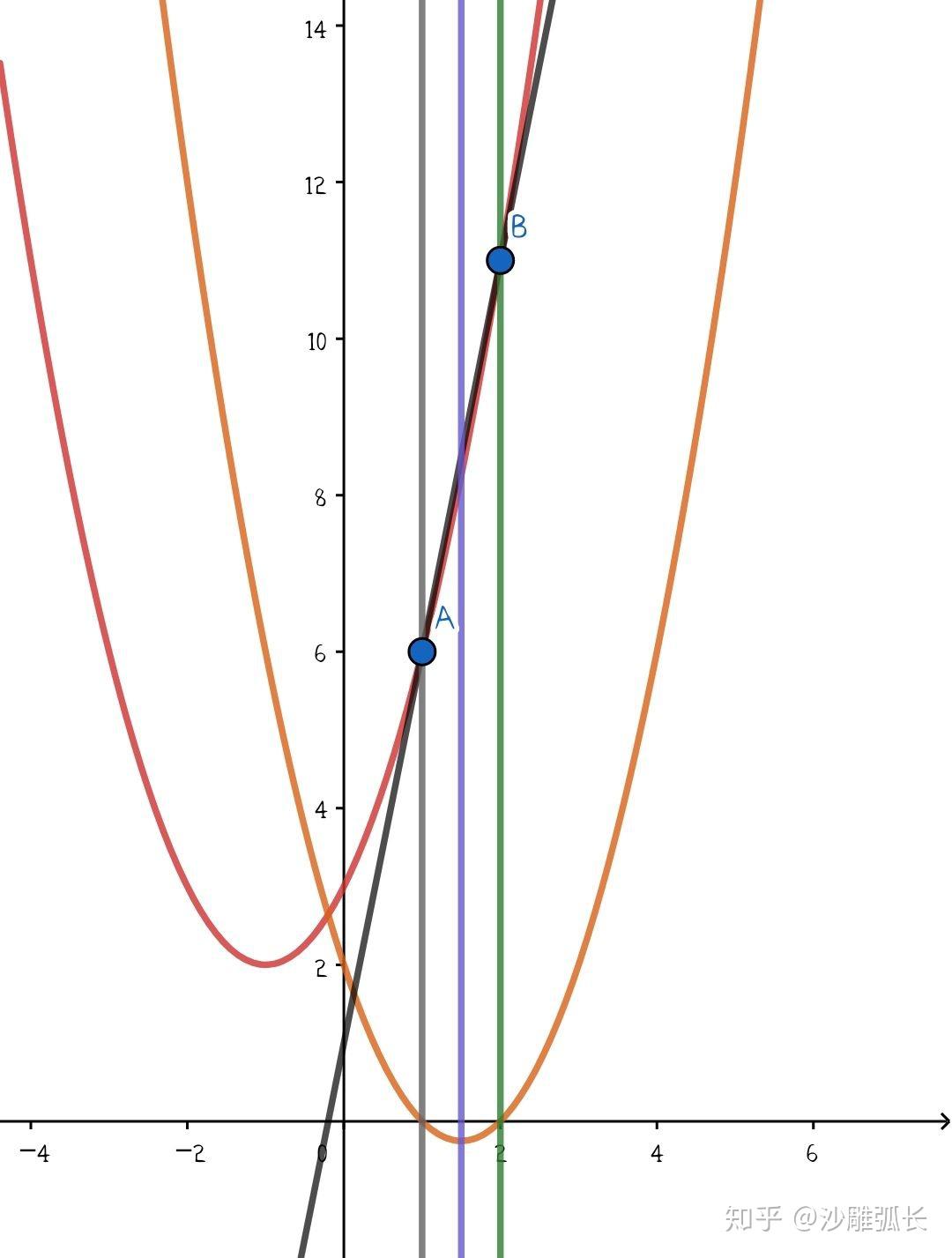
1.平行六面体和三棱锥体积公式拓展

$V=\\left| \\begin{matrix} a_1& a_2& a_3\\\\ b_1& b_2& b_3\\\\ c_1& c_2& c_3\\\\ \\end{matrix}\\right|$ (a1,a2……c2,c3同初中篇结论一，是向量的分量)

三棱柱除以二即可

至于 $\\left| \\begin{matrix} a_1& a_2& a_3\\\\ b_1& b_2& b_3\\\\ c_1& c_2& c_3\\\\ \\end{matrix}\\right|$ 叫做三阶行列式，求法可以查找线性代数资料，前五页就会讲

https://www.wanweibaike.com/wiki-行列式

eg:
$求A(1,4),B(5,3),C(7,6),D(10,2)为顶点的三棱锥体积$

2.泰勒展开式列举

泰勒展开式:
$f(x)={\\displaystyle \\sum _{n=0}^{\\infty }{\\frac{f^{(n)}(a)}{n!}}(x-a)^{n}}$
麦克劳林展开式:
$f(x)={\\displaystyle \\sum _{n=0}^{\\infty }{\\frac{f^{(n)}(0)}{n!}}x^{n}}$
其中 $n!$ 表示n的阶乘, $f^{(n)}$ 表示n阶导

eg:

常用的

${\\displaystyle e^{x}=\\sum _{n=0}^{\\infty }{\\frac{x^{n}}{n!}}=1+x+{\\frac{x^{2}}{2!}}+{\\frac{x^{3}}{3!}}+\\cdots +{\\frac{x^{n}}{n!}}+\\cdots \\quad \\forall x}$
${\\displaystyle \\ln(1+x)=\\sum _{n=1}^{\\infty }{\\frac{(-1)^{n+1}}{n}}x^{n}=x-{\\frac{x^{2}}{2}}+{\\frac{x^{3}}{3}}-\\cdots +{\\frac{(-1)^{n+1}}{n}}x^{n}+\\cdots \\quad \\forall x\\in (-1,1]}$
${\\displaystyle \\ln(1-x)=-\\sum _{n=1}^{\\infty }{\\frac{x^{n}}{n}}=-x-{\\frac{x^{2}}{2}}-{\\frac{x^{3}}{3}}-\\cdots -{\\frac{x^{n}}{n}}-\\cdots \\quad \\forall x\\in[-1,1)}$
${\\displaystyle{\\begin{aligned}\\sin x&=\\sum _{n=0}^{\\infty }{\\frac{(-1)^{n}}{(2n+1)!}}x^{2n+1}&&=x-{\\frac{x^{3}}{3!}}+{\\frac{x^{5}}{5!}}-\\cdots &&\\forall x\\\\[6pt]\\cos x&=\\sum _{n=0}^{\\infty }{\\frac{(-1)^{n}}{(2n)!}}x^{2n}&&=1-{\\frac{x^{2}}{2!}}+{\\frac{x^{4}}{4!}}-\\cdots &&\\forall x\\\\[6pt]\ an x&=\\sum _{n=1}^{\\infty }{\\frac{B_{2n}(-4)^{n}\\left(1-4^{n}\\right)}{(2n)!}}x^{2n-1}&&=x+{\\frac{x^{3}}{3}}+{\\frac{2x^{5}}{15}}+\\cdots &&\\forall x:|x|<{\\frac{\\pi }{2}}\\\\[6pt]\\sec x&=\\sum _{n=0}^{\\infty }{\\frac{(-1)^{n}E_{2n}}{(2n)!}}x^{2n}&&=1+{\\frac{x^{2}}{2}}+{\\frac{5x^{4}}{24}}+\\cdots &&\\forall x:|x|<{\\frac{\\pi }{2}}\\\\[6pt]\\arcsin x&=\\sum _{n=0}^{\\infty }{\\frac{(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x+{\\frac{x^{3}}{6}}+{\\frac{3x^{5}}{40}}+\\cdots &&\\forall x:|x|\\leq 1\\\\[6pt]\\arccos x&={\\frac{\\pi }{2}}-\\arcsin x\\\\&={\\frac{\\pi }{2}}-\\sum _{n=0}^{\\infty }{\\frac{(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&={\\frac{\\pi }{2}}-x-{\\frac{x^{3}}{6}}-{\\frac{3x^{5}}{40}}+\\cdots &&\\forall x:|x|\\leq 1\\\\[6pt]\\arctan x&=\\sum _{n=0}^{\\infty }{\\frac{(-1)^{n}}{2n+1}}x^{2n+1}&&=x-{\\frac{x^{3}}{3}}+{\\frac{x^{5}}{5}}-\\cdots &&\\forall x:|x|\\leq 1,\\ x\ eq \\pm i\\end{aligned}}}$

和不常用的

${\\displaystyle \\sinh x=\\sum _{n=0}^{\\infty }{\\frac{1}{(2n+1)!}}x^{2n+1}\\quad \\forall x}$
${\\displaystyle \\cosh x=\\sum _{n=0}^{\\infty }{\\frac{1}{(2n)!}}x^{2n}\\quad \\forall x}$
${\\displaystyle \ anh x=\\sum _{n=1}^{\\infty }{\\frac{B_{2n}4^{n}(4^{n}-1)}{(2n)!}}x^{2n-1}\\quad \\forall x:\\left|x\\right|<{\\frac{\\pi }{2}}}$
${\\displaystyle \\sinh ^{-1}x=\\sum _{n=0}^{\\infty }{\\frac{(-1)^{n}(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}\\quad \\forall x:\\left|x\\right|<1}$
${\\displaystyle \ anh ^{-1}x=\\sum _{n=0}^{\\infty }{\\frac{1}{2n+1}}x^{2n+1}\\quad \\forall x:\\left|x\\right|<1}$

如果感兴趣，可以研究这个(多元泰勒展开)

$f(x_1,...,x_d)={\\displaystyle \\sum _{n_{1}=0}^{\\infty }\\cdots \\sum _{n_{d}=0}^{\\infty }{\\frac{\\partial ^{n_{1}+\\cdots +n_{d}}}{\\partial x_{1}^{n_{1}}\\cdots \\partial x_{d}^{n_{d}}}}{\\frac{f(a_{1},\\cdots ,a_{d})}{n_{1}!\\cdots n_{d}!}}(x_{1}-a_{1})^{n_{1}}\\cdots (x_{d}-a_{d})^{n_{d}}}$

还是举个例子吧

eg:
$已知x>0,\\frac{e^x-1}{x}\\geq ax+1，求a的范围$
sol:
$\ ext{左右乘一个}x \\\\ \ ext{得到}e^x-1-x-\\frac{ax^2}{2}\\ge 0 \\\\ \ ext{又}e^x=\\sum_{n=0}^{\\infty}{\\frac{x^n}{n!}}=1+x+\\frac{x^2}{2!}+\\frac{x^3}{3!}+\\cdots +\\frac{x^n}{n!}+\\cdots \\quad \\\\ \ ext{得到}\\left( \\frac{1}{2}-\\frac{a}{2}\\right) x^2+\\frac{x^3}{3!}+\\cdots +\\frac{x^n}{n!}+\\cdots \\ge 0 \\\\ x=0,\ ext{取得}a\ ext{最大值}\\\\ \ ext{则得到}a\\le 1$
$(题目摘录于-高考导数放缩专练题)$
方法原创

启示:一般遇到导数放缩题可以考虑泰勒展开化简

草草结尾/笑

(中考前最后一篇文章)~

——written by huchang

QS 2020中上榜的台湾高校

新加坡留学，公立大学or私立大学，哪个更适合自己？